Question

In an office, every employee likes at least one of tea, coffee, and milk. The number of employees who like only tea, only coffee, only milk and all the three is all equal to x. The number of employees who like only tea and coffee, only coffee and milk, and only tea and milk is equal and each is equal to the number of employees who like all three is equal to x. Then the possible value of the number of employees on the office is
(A) 65
(B) 90
(C) 77
(D) 85

Answer 1

Hint: The number of employees who like only Tea, Coffee, and Milk is equal to x. The number of employees who like only tea and coffee, only coffee and tea, and only tea and milk is equal to x. The number of employees who like all three is equal to x, $\left( T\cap C\cap M \right)$ = x. Using these all pieces of information, draw a Venn diagram. Now, get the total number of employees who are included in the tea circle, coffee circle, and milk circle that is, $n\left( T \right)$ , $n\left( C \right)$ , and $n\left( M \right)$ respectively. Then, get the total number of employees who are included in the tea and coffee circle, coffee and milk circle, and tea and milk circle that is, $n\left( T\cap C \right)$ , $n\left( C\cap M \right)$ , and $n\left( T\cap M \right)$ respectively. We have to get the total number of employees that is $\left( T\cap C\cap M \right)$ . Use the formula,
$T\cup C\cup M=n\left( T \right)+n\left( C \right)+n\left( M \right)-n\left( T\cap C \right)-n\left( C\cap M \right)-n\left( T\cap M \right)+\left( T\cap C\cap M \right)$ and solve it further.

Complete step-by-step answer:
According to the question, it is given that, in an office, The number of employees who like only tea, only coffee, only milk and all the three is all equal to x. So,
The number of employees who like only Tea = x.
The number of employees who like only Coffee = x.
The number of employees who like only Milk = x.
It is also given that, the number of employees who like only tea and coffee, only coffee and milk and only tea and milk is equal and each is equal to the number of employees who like all the three is equal to x. So,
The number of employees who like only tea and coffee, $n\left( T\cap C \right)$ = x …………………..(1)
The number of employees who like only coffee and milk, $n\left( C\cap M \right)$ = x ……………………(2)
The number of employees who like only tea and milk, $n\left( T\cap M \right)$ = x ………………………..(3)
The number of employees who like tea, coffee, and milk, $\left( T\cap C\cap M \right)$ = x ………………….(4)
Now, drawing Venn diagram, we get

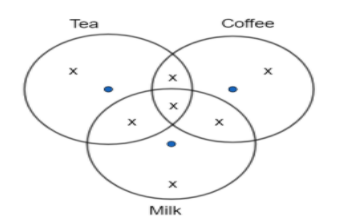
In the Venn diagram, we have,
The total number of employees who are included in the tea circle, $n\left( T \right)$ = 4x ………………………..(5)
The total number of employees who are included in the coffee circle, $n\left( C \right)$ = 4x ……………………..(6)
The total number of employees who are included in the milk circle, $n\left( M \right)$ = 4x ……………………………(7)
The total number of employees who are included in tea and coffee circle, $n\left( T\cap C \right)$ = 2x …………………..(8)
The total number of employees who are included in coffee and milk circle, $n\left( C\cap M \right)$ = 2x ……………………(9)
The total number of employees who are included in tea and milk circle, $n\left( T\cap M \right)$ = 2x
………………………..(10)
The total number of employees can be expressed as $\left( T\cap C\cap M \right)$ .
We know the formula,
$A\cup B\cup C=n\left( A \right)+n\left( B \right)+n\left( C \right)-n\left( A\cap B \right)-n\left( B\cap C \right)-n\left( A\cap C \right)+\left( A\cap B\cap C \right)$ ……………..(11)
Replacing A by T, B by C, and C by M in equation (8), we get
$T\cup C\cup M=n\left( T \right)+n\left( C \right)+n\left( M \right)-n\left( T\cap C \right)-n\left( C\cap M \right)-n\left( T\cap M \right)+\left( T\cap C\cap M \right)$ ……………………..(12)
From equation (4), equation (5), equation (6), equation (7), equation (8), equation (9), equation (10), and equation (12), we get

& T\cup C\cup M=n\left( T \right)+n\left( C \right)+n\left( M \right)-n\left( T\cap C \right)-n\left( C\cap M \right)-n\left( T\cap M \right)+\left( T\cap C\cap M \right) \\\ & \Rightarrow T\cup C\cup M=4x+4x+4x-2x-2x-2x+x \\\ \end{aligned}$$ $$\Rightarrow T\cup C\cup M=7x$$ ……………………..(13) In equation (13), we have the total number of employees equal to 7x. We can see that the total number of employees is multiple of 7. Among all the options given, we have the only option (C) which is the multiple of 7. So, the correct option is (C). Note: In this question, one can take the total number of employees who like tea, coffee, and milk as x. This is wrong. ‘x’ is the number of employees who like only tea, only coffee, and only milk. The number of employees who like only tea, only coffee, and only milk cannot be equal to the total number of employees who like tea, coffee, and milk. To get the total number of employees who like tea, coffee, and milk, we have to draw the Venn diagram.