Question

In an $LCR$ series a.c. circuit, the voltage across each of the components $L,{\text{ }}C$ and $R$ is $50{\text{ }}V$. The voltage across the $LC$ combination will be:
A) $50 V$
B) $50\sqrt 2 V$
C) $100 V$
D) $0 V$ (zero)

Answer 1

In $LCR$ series a.c circuit, the components $L,{\text{ }}C$ and $R$ are related to each other in a way that the voltage across the inductor $L$(${V_L}$) and voltage across the capacitor $C$(${V_C}$) has a constant phase difference. The voltage across the resistance $R$(${V_R}$) and current($i$) does not have any phase difference.

Complete step by step solution:
According to the question, a $LCR$ series a.c. circuit is given. The voltage across $L,{\text{ }}C$ and $R$ is $50{\text{ }}V$.

We know that in an $LCR$ series circuit, the voltage across the inductor $L$(${V_L}$) leads the current($i$) by ${90^ \circ }$ and voltage across the capacitor $C$(${V_C}$) lags the current($i$) by ${90^ \circ }$. So, the inductance and the capacitance are in opposite phases. In an $LCR$ series circuit, the voltage across the resistance $R$(${V_R}$) is in the same phase with current($i$).
So, the voltage across the $LC$ combination will be given as:
${V_{LC}} = {V_L} - {V_C} \\\ \Rightarrow {V_{LC}} = 50 - 50 \\\ \Rightarrow {V_{LC}} = 0 \\\$
To understand the phase difference in different voltages, we can make a graph which shows the phase difference between voltages.

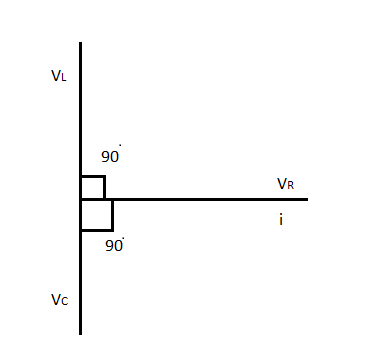
According to the above graph, ${V_R}$ and $i$ are in the same phase. ${V_L}$leads current $i$ by ${90^ \circ }$ and ${V_C}$ lags current $i$ by ${90^ \circ }$. So, the voltage across $LC$ combination is zero.

Hence, option (D) is correct.

Note: Voltage across the inductor ${V_L}$ and current $i$ has a phase difference. Voltage across the capacitor ${V_C}$ and current $i$ has a phase difference. The voltage across the resistance ${V_R}$ and current $i$ has zero phase difference. According to the graph, current $i$ and voltage across the resistance ${V_R}$ are plotted on X-axis.