Question

In an LCR circuit as shown below, both the switches are open initially. Now, switch S1 is closed and S2 is kept open (q is the charge on the capacitor and $\tau$=RC is capacitance time constant). Which of the following statements is correct?

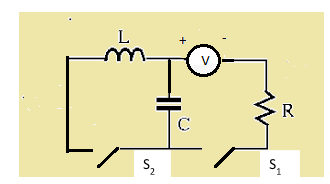
1. Work done by the battery is half of the energy dissipated in the resistor.
2. At t=$\tau$, q=CV/2
3. At t= 2$\tau$, q=CV (1-e-2)
4. At t= $\dfrac{\tau }{2}$, q=CV(1-e-1)

Answer 1

We will use the property of capacitors that a steady state capacitor will act as an open circuit because at steady state current through the capacitor will be zero, which shows transient behaviour.
Inductor will play no role in the circuit as the switch S2 will remain closed.
The above concepts will help us in solving the problem.

Complete step by step solution:
Capacitors have transient properties in which capacitors act as short circuits before closing the switch S, which means the capacitor has no charge before closing the switch S voltage across the capacitor is zero.
By the time the capacitor gets charged after closing the switch voltage across the capacitor keeps on increasing and current becomes zero.
Now come to the calculation part of the charge:
In transient behaviour when capacitor is charged voltage appears across it is given as:
$V = {V_0}\left( {1 - {e^{ - \dfrac{t}{\tau }}}} \right)$ similarly, if we have to calculate charge it is given as:
$q = C{V_0}\left( {1 - {e^{ - \dfrac{t}{\tau }}}} \right)$...............2
At t = 2$\tau$ charge becomes;
$\Rightarrow q = C{V_0}\left( {1 - {e^{ - \dfrac{{2\tau }}{\tau }}}} \right) \\\ \therefore q = C{V_0}\left( {1 - {e^{ - 2}}} \right) \\\$(we have substituted 2$\tau$in the equation 2 and cancelled both $\tau$)
Option 3 is the correct one.

Note: Like capacitors have transient properties similarly inductors too have transient properties .When the switch is open current through the inductor is zero and acts as an open circuit. When the switch is closed, the steady state voltage across the inductor will be zero and current reaches its maximum peak. When current becomes zero across an element it behaves as an open circuit and when voltage across an element becomes zero it acts as a short circuit.