Solveeit Logo
Login

Question

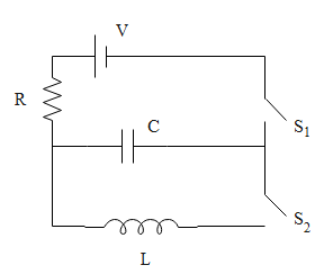
Question: In an LCR circuit as shown below both switches are open initially. Now switch \({S_1}\) is closed, \...

In an LCR circuit as shown below both switches are open initially. Now switch S1{S_1} is closed, S2{S_2} kept open. (q is charged on the capacitor and τ=RC\tau = RC is a capacitive time constant). Which of the following statements is correct?

A. At t=τ, q=CV2t = \tau ,{\text{ }}q = \dfrac{{CV}}{2}
B. At t=2τ, q=CV(1−e−2)t = 2\tau ,{\text{ }}q = CV\left( {1 - {e^{ - 2}}} \right)
C. At t=τ2, q=CV(1−e−1)t = \dfrac{\tau }{2},{\text{ }}q = CV\left( {1 - {e^{ - 1}}} \right)
D. Work done by the battery is half of the energy dissipated in the resistor.

Explanation

Solution

When the switch S1{S_1} is closed, then current flows through the capacitor. By using the expression for charge on a capacitor as a function of time and inserting different values of time as given in options, we can check which option is correct.
Formula used:
The expression for charge on a capacitor at a given time t is given as
q=CV(1−e−t/τ)q = CV\left( {1 - {e^{ - t/\tau }}} \right)

Complete answer:
We are given an LCR circuit which has two switches. Initially the switches are open but then switch S1{S_1} is closed, S2{S_2} kept open. On the closing switch S1{S_1}, the current flows through the circuit containing the capacitor.
As the switch is turned on, the capacitor will start charging and slowing the charge will start building up in the capacitor. The expression which gives us charge on the capacitor at any time t is given as
q=CV(1−e−t/τ)q = CV\left( {1 - {e^{ - t/\tau }}} \right)
Here C is the capacitance of the capacitor, V represents the voltage on the capacitor and τ=RC\tau = RC is a capacitive time constant.
Now let us check the charge on the capacitor at different values of t.
At t=τ, q=CV(1−e−τ/τ)=CV(1−e−1)t = \tau ,{\text{ }}q = CV\left( {1 - {e^{ - \tau /\tau }}} \right) = CV\left( {1 - {e^{ - 1}}} \right)
At t=2τ, q=CV(1−e−2τ/τ)=CV(1−e−2)t = 2\tau ,{\text{ }}q = CV\left( {1 - {e^{ - 2\tau /\tau }}} \right) = CV\left( {1 - {e^{ - 2}}} \right)
At t=τ2, q=CV(1−e−12)t = \dfrac{\tau }{2},{\text{ }}q = CV\left( {1 - {e^{ - \dfrac{1}{2}}}} \right)
The work done by a capacitor is U=12CV2U = \dfrac{1}{2}C{V^2} while the work done by a resistor is W=I2Rt=VItW = {I^2}Rt = VIt. These two are not equal so the total work done by battery is not equal to half of the energy dissipated in the resistor.

Hence, we can say that the correct answer is option B.

Note:
When we turn only switch S1{S_1} on, then the inductor does not get involved in the circuit and we are left with only an RC circuit. In case if we turn switch S2{S_2} also on, then we will need to take the inductor in consideration for calculating charge on the capacitor.