Question

In an isosceles triangle ABC, the vertex A is $(6, 1)$ and the equation of the base BC is $2x + y = 4$. Let the point B lie on the line $x + 3y = 7$. If $(α, β)$ is the centroid of ΔABC, then $15(α + β)$ is equal to :

• A. 39
• B. 41
• C. 51
• D. 63

Answer 1

Answer: (C)

51

Answer 2

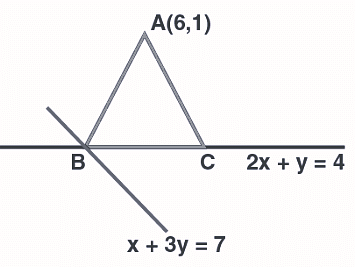
$2x+y = 4$ …….. (1)
$2x+6y = 14$ …….. (2)
On solving eq(1) and eq(2)
$y = 2, \ x = 3$
$B(1, 2)$ and $C(k, 4 – 2k)$
Hence, $AB^2 = AC^2$
$52 \+ (–1)^2 = (6 – k)^2 \+ (–3 + 2k)^2$
$⇒ 5k^2 – 24k \+ 19 = 0$
$(5k – 19)(k – 1) = 0$
⇒ k=$$\frac {19}{5}

$C$ $(\frac {19}{5}$,−$\frac {18}{5})$ ⇒ Centroid $(α, β)$

$α = \frac {6+1+\frac {19}{5}}{3}$
$α = \frac {18}{5}$
$β = \frac {1+2-\frac {18}{5}}{3}$

$β= -\frac 15$

Now $15(α + β)$ $= 15(\frac {18}{5}+(-\frac 15))$
$=15 \times \frac {17}{5}$
$= 51$

So, the answer is (C): $51$.