Question

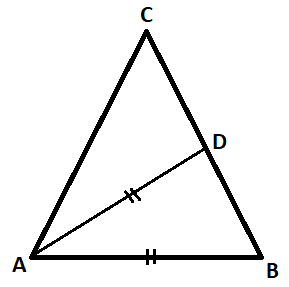
In an isosceles triangle $ABC,AC = BC,\angle BAC$ is bisected by AD where D lies on BC. It is found that AD = AB. Then $\angle ACB$ equals

A. ${72^ \circ }$
B. ${54^ \circ }$
C. ${36^ \circ }$
D. ${60^ \circ }$

Answer 1

This is a simple problem, to solve this problem we have to know about some basic properties of triangles, such as properties of an isosceles triangle, which are any two sides of an isosceles triangle are equal and also the angles which are opposite to the equal sides are equal. One more important thing is that the sum of the angles in any triangle is equal to ${180^ \circ }.$

Complete step by step answer:
Here $\angle ACB = \angle C$ and
$\angle BAC = \angle A$
Given that the triangle ABC is an isosceles triangle. The sides AC is equal to BC, as given below:
$\Rightarrow AC = BC$
Which means that the angles opposite to the sides AC and BC are also equal which is a property of an isosceles triangle.
$\therefore \angle A = \angle B$
Let $\angle A = \angle B = x$
Here given that the angle $\angle A$ is bisected by a line segment AD.
Now given that AD = AB, which means that now a new triangle ADB is formed which is also an isosceles triangle.
As the triangle ADB is an isosceles triangle, hence the angles opposite to the sides AD and AB are also equal, which are given below:
$\Rightarrow \angle ADB = \angle B$
We know that $\angle B = x$
$\therefore \angle ADB = x$
Now given that the line segment AD bisects the angle $\angle A$, hence the angle $\angle DAB$ is given by:
$\Rightarrow \angle DAB = \dfrac{{\angle A}}{2}$
$\because \angle A = x$
$\therefore \angle DAB = \dfrac{x}{2}$
Now every triangle should follow the property that the sum of the angles in a triangle should be equal to ${180^ \circ }$.
Consider the triangle ADB, the sum of angles in this triangle should sum up to give ${180^ \circ }$, as given below:
$\Rightarrow \angle DAB + \angle B + \angle ADB = {180^ \circ }$
$\Rightarrow \dfrac{x}{2} + x + x = {180^ \circ }$
$\Rightarrow \dfrac{{5x}}{2} = {180^ \circ }$
$\Rightarrow x = {72^ \circ }$
$\therefore \angle A = \angle B = {72^ \circ }$
Now consider the triangle ABC, the sum of all the angles in this triangle should be equal to ${180^ \circ }$.
$\Rightarrow \angle A + \angle B + \angle C = {180^ \circ }$
$\Rightarrow {72^ \circ } + {72^ \circ } + \angle C = {180^ \circ }$
$\Rightarrow \angle C = {180^ \circ } - {144^ \circ }$
$\Rightarrow \angle C = {36^ \circ }$
$\because \angle C = \angle ACB$
$\therefore \angle ACB = {36^ \circ }$

$\angle ACB$ equals ${36^ \circ }$.

Note: Here while solving this problem there is a slight chance of overlooking the given hint such as given that the sides AD and AB are equal in the triangle ADB. Here as it is given that AD and AB are equal, hence the angles opposite to the sides AD and AB are equal. This is an important and the most crucial step, as it leads to the rest of the process.