Question

In an isosceles triangle ABC; AB = AC = 10cm and BC = 18 cm. Find the value of: ${{\tan }^{2}}C-{{\sec }^{2}}B+2$.

Answer 1

Hint: Use property of an isosceles triangle which is given as opposite angles of the two sides are equal if sides are equal. Now, use sine rule to find the value of the given expression. Sine rule is given as
$\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}$

Complete step-by-step answer:
Here, we have an isosceles triangle ABC, such that AB = AC = 10cm and BC = 18cm. And need to determine the value of ${{\tan }^{2}}C-{{\sec }^{2}}B+2=?$
We know the property of an isosceles triangle that the opposite angles of the equal opposite side are equal to each other.
As AB = AC =10cm, hence $\angle B=\angle C$ by the above property.
Let $\angle B=\angle C=\theta$ and hence $\angle A$ is given as ${{180}^{o}}-2\theta$ by the property of triangle that sum of interior angles of a triangle is ${{180}^{\circ }}.$ Hence we get
$\begin{aligned} & \angle B=\angle C=\theta \\\ & \Rightarrow \angle A={{180}^{o}}-2\theta \\\ \end{aligned}$
AB = AC = 10cm, BC = 18cm
The diagram for the triangle is as shown below:

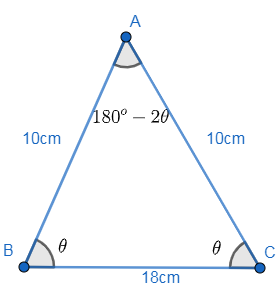
So, we can apply ‘sine rule’ to calculate the given expression. Sine rule of any triangle ABC is given as
$\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}...........\left( i \right)$
Here a, b, c are opposite sides to the angles $\angle A,\angle B,\angle C.$
Hence, from the equation (i), we get
$\dfrac{\sin \left( {{180}^{o}}-2\theta \right)}{18}=\dfrac{\sin \theta }{10}=\dfrac{\sin \theta }{10}$
$\Rightarrow \dfrac{\sin \left( {{180}^{o}}-2\theta \right)}{18}=\dfrac{\sin \theta }{10}................\left( ii \right)$
Now, we can replace $\sin \left( {{180}^{\circ }}-2\theta \right)$ by $\sin 2\theta$ by the identity, $\sin \left( 180-\theta \right)=\sin \theta$.
Hence, we get equation (ii) as,
$\dfrac{\sin 2\theta }{18}=\dfrac{\sin \theta }{10}$
Now, use trigonometric identity $\sin 2\theta =2\sin \theta \cos \theta$. Hence, we get
$\dfrac{2\sin \theta \cos \theta }{18}=\dfrac{\sin \theta }{10}$
Cancelling the like terms, we get
$\dfrac{2\cos \theta }{18}=\dfrac{1}{10}$
$\Rightarrow \cos \theta =\dfrac{9}{10}.................\left( iii \right)$
Now, replace $\theta$ by B, we get
$\cos B=\dfrac{9}{10}$
Now we know $\sec \theta =\dfrac{1}{\cos \theta }$ , so we get
$\sec B=\dfrac{10}{9}..................\left( iv \right)$
Now we know by Pythagoras theorem,
${{\left( Hypotenuse \right)}^{2}}={{(base)}^{2}}+{{(perpendicular)}^{2}}.........(v)$
Now we know, $\cos B=\dfrac{9}{10}=\dfrac{base}{hypotenuse}$, substituting these values in equation (v), we get
$\begin{aligned} & {{\left( 10 \right)}^{2}}={{(9)}^{2}}+{{(perpendicular)}^{2}} \\\ & \Rightarrow perpendicular=\sqrt{100-81}=\sqrt{19} \\\ \end{aligned}$
So, we can write,
$\tan B=\dfrac{\text{Perpendicular}}{\text{Base}}=\dfrac{\sqrt{19}}{9}...................\left( vi \right)$
Now, we can solve the expression ${{\tan }^{2}}C-{{\sec }^{2}}B+2.$ Let it’s value be ‘M’. Hence we get,
$M={{\tan }^{2}}C-{{\sec }^{2}}B+2$
Now, we know that $\angle B=\angle C$ (isosceles triangle), so we can write
$M={{\tan }^{2}}B-{{\sec }^{2}}B+2$
Now, put values of $\tan B$ and $\sec B$ from the equation (iv) and (vi) hence, we get
$M={{\left( \dfrac{\sqrt{19}}{9} \right)}^{2}}-{{\left( \dfrac{10}{9} \right)}^{2}}+2$
$\Rightarrow M=\dfrac{19}{81}-\dfrac{100}{81}+2$
$\begin{aligned} & \Rightarrow M=\dfrac{19-100}{81}+2 \\\ & \Rightarrow M=\dfrac{-81}{81}+2=-1+2=1 \\\ \end{aligned}$
So, the value of ${{\tan }^{2}}C-{{\sec }^{2}}B+2$ is 1.

Note: One can calculate value of $\tan C$and $\sec B$ , using the cosine formula as well which is given as, $\cos \theta =\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$
Here $\theta$ is the angle between side ’b’ and ‘c’.
Another approach is when we find the value of $\sec \theta$ , we can calculate the value of $\tan \theta$ using the formula, ${{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta$.