Question
Question: In an experiment using tangent galvanometer, the magnetic induction is measured at various points on...
In an experiment using tangent galvanometer, the magnetic induction is measured at various points on the axis of a current carrying circular coil on both sides of the center O of the coil. The variation of magnetic field along the axis is best represented in the curve:
A. 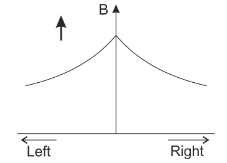
B. 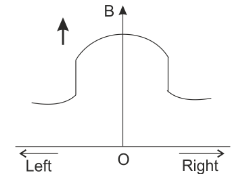
C. 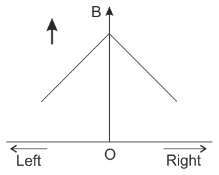
D. 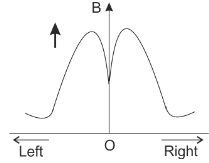
Solution
In a current carrying coil the electric current creates a magnetic field which is more concentrated in the center of the coil than outside the loop. According to Biot-Savart’s law, the magnetic field at a point due to an element of a conductor carrying current is,
-Directly proportional to the strength of the current.
-Directly proportional to the length of the element.
-Directly proportional to the Sine of the angle between the element and the line joining the element to the point.
-Inversely proportional to the square of the distance between the element and the point.
Complete step by step answer:
Let us assume that the radius of the coil be R.
Then the magnetic field at distance r on the axis of coil is given by,
B=2(r2+R2)23μoIR2
Now when r>>R
B=2r3μoIR2
Since radius of the coil and current are constant we can say that,
B∝r31......(1)
Now at the center of the coil we have,
r=R
Hence, the expression for magnetic field becomes
B = \dfrac{{{\mu _o}I{r^2}}}{{{r^3}}} \\\
\Rightarrow B = \dfrac{{{\mu _o}I}}{r} \\\
Since, current is constant Therefore, we have
B∝r1......(2)
From (1) and (2) we can observe that the plot for magnetic field due to current carrying coil is
