Question

In an experiment to measure the speed of light by Fizeau’s apparatus, the following data are used:
Distance between the mirrors = 12 km
Number of teeth in the wheel = 180
Find the minimum angular speed of the wheel for which the image is not seen.

Answer 1

This is a direct question. Fizeau’s apparatus is used to measure the speed of light by making use of two mirrors, a toothed wheel and a source of light. Using Fizeau’s equation, which relates the distance between the mirrors, the number of teeth in the wheel and the angular speed of the wheel, the value of angular speed can be calculated.

Formula used:
$c=\dfrac{2Dnw}{\pi }$

Complete step-by-step answer:
Fizeau apparatus diagram is as follows.

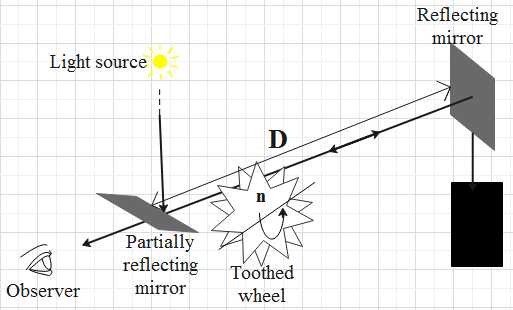
The formula that relates the angular speed of the wheel with the distance between the mirrors and the number of teeth in the wheel is as follows.

$c=\dfrac{2Dnw}{\pi }$
Where D is the distance between the mirrors, w is the angular speed of the wheel, n is the number of teeth in the wheel and c is the speed of light in air.

Firstly, express the formula in terms of the angular speed of the wheel.
$w=\dfrac{c\pi }{2nD}\,{rad}/{s}\;$
The above expression represents the angular speed of the wheel in terms of radians per second. So, we need to change it to a degree per second.

In order to do that, we need to multiply and divide the above equation with 180 by pi. Thus, we get,
$w=\dfrac{c\pi }{2nD}\times \dfrac{180}{\pi }\,\,{\deg }/{s}\;$

From given, we have the data,
Distance between the mirrors = 12 km
$\Rightarrow D=12\times {{10}^{3}}m$
Number of teeth in the wheel = 180
$\Rightarrow n=180$

Substitute the given values in the above equation to find the value of the angular speed of the wheel.
Thus, we have,

& w=\dfrac{c}{2nD}\times 180 \\\ & \Rightarrow w=\dfrac{3\times {{10}^{8}}}{2\times 180\times 12\times {{10}^{3}}}\times 180 \\\ \end{aligned}$$ Upon continue the further calculation, we get, $$w=1.25\times 10{}^{4}\,\,{\deg }/{s}\;$$ Therefore, the minimum angular speed of the wheel for which the image is not seen is $$1.25\times 10{}^{4}\,\,{\deg }/{s}\;$$. **Note:** The units of the parameters should be taken care of. As in this question, we have to change the unit of the distance between the mirrors from km to m, as the speed of the light will be in terms of meters per second. Even, instead of the angular speed, the distance between the mirrors or the number of teeth in the wheel can be asked, giving the values of the other two parameters.