Question
Question: In an experiment to find the focal length of a concave mirror, a graph is drawn between the magnitud...
In an experiment to find the focal length of a concave mirror, a graph is drawn between the magnitudes of u and v. The graph looks like:
A)
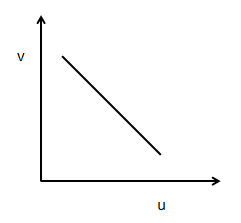
B)
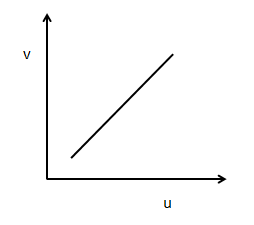
C)
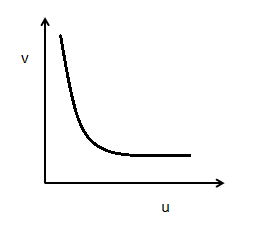
D)
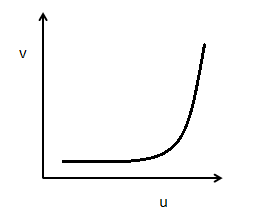
Solution
The image formed is real and inverted when the object is placed in front of a concave mirror and beyond the principal focus of the mirror. In the case of graphs, initially finding the relation between slope, image distance, object distance. to find the nature of the curve.
Complete step by step answer:
The relation between the object distance u, the image distance v and the focal length f of the mirror is known as mirror formula. It is given by,
⇒f1=u1+v1
It is valid for the both concave and convex mirrors, whether the image formed is real or virtual.
Mirror equation can also be written as,
⇒u1=f1−v1……………….(1)
Graph is plotted by taking image distance v along y-axis and object distance ualong x-axis.
Slope of the given graphs is written as,
⇒slope=X−scaleY−scale
In the graph the slope can be written as the image distance divided by the object distance.
⇒slope=dudv …………………(2)
Now lets us consider equation (1), and differentiate that equation we get,
Using quotient rule,
⇒dxd(vu)=v2v.dxdu−u.dxdv
By doing the simplifications we get,
⇒v2vdu−vdv
Apply this formula, we get
⇒u2u.d(1)−1.du=f2f.d(1)−1.df−v2v.d(1)−1.dv
Differentiation of constants gives us zero.
After solving we get,
⇒u2−1du=0−v2−1dv
Then,
⇒u2−1du=v21dv
Rearranging the above equation, we get,
⇒dudv=−u2v2 …………………(3)
Now comparing equation (2) and (3) we get
⇒slope=−u2v2
dudv is the slope, that is negative. Therefore, either the curve (C) or the curve (A) is right. Since curves (B) and (D) have a positive slope that cannot be done here.
Slope now relies on the u and v values. That is, as per the equation above, it continues to change at any point. So, figure (C) is the correct option.
So, figure (C) is the correct option.
∴ Correct option is (C).
Note: Focal length of a mirror is the distance between the principal focus and the pole of the mirror. it is denoted by ‘f’
Image distance is the distance between the pole of the mirror and image formed. It is denoted by ‘v’.
Object distance is the distance between the pole of the mirror and object placed. It is denoted by ‘u’.
