Question

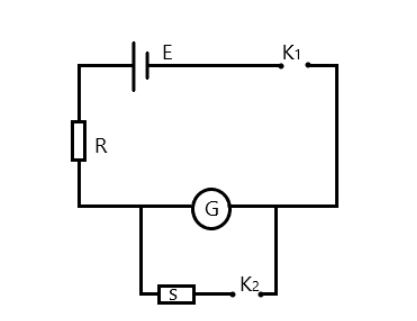
In an experiment to determine the resistance of a galvanometer by half deflection method, the circuit shown is used. In one set of readings, if $R = 10\Omega$ and $S = 4\Omega$, then the resistance of the galvanometer is:

(A) $\dfrac{{20}}{3}\Omega$
(B) $\dfrac{{40}}{3}\Omega$
(C) $\dfrac{{50}}{3}\Omega$
(D) $\dfrac{{70}}{3}\Omega$

Answer 1

In half deflection method, the value of the resistance across the resistor is such that the deflection made will be half that of the current when the resistance was disconnected. The current is directly proportional to the deflection of a galvanometer pointer.
Formula used: In this solution we will be using the following formulae;
$G = \dfrac{{RS}}{{R - S}}$ where $G$ is the resistance of the galvanometer, $R$ is the resistance in the main circuit and $S$ is the resistance across the galvanometer

Complete step by step solution:
Generally, the formula using half deflection method the resistance of a galvanometer is given as
$G = \dfrac{{RS}}{{R - S}}$ where $G$ is the resistance of the galvanometer, $R$ is the resistance in the main circuit and $S$ is the resistance across the galvanometer
Hence, by inserting known values, we have
$G = \dfrac{{10\left( 4 \right)}}{{10 - 4}} = \dfrac{{40}}{6}\Omega$
$\Rightarrow G = \dfrac{{20}}{3}\Omega$

Hence, the correct option is A

Note: For clarity, the formula used can be proven as follows:
First, let’s assume the key ${K_1}$ is the only closed key. In this case the current flowing through the circuit, and hence through $G$ will be
${I_G} = \dfrac{E}{{R + G}}$
Generally, the deflection shown in the galvanometer is proportional to the current flowing through it. Hence,
${I_G} = k\theta$
Then
$\dfrac{S}{{S + G}}I = \dfrac{{k\theta }}{2}$
Now, assuming we close the key ${K_2}$, it can be proven that the current flowing through the galvanometer becomes
$I{'_G} = \dfrac{S}{{S + G}}I$where$I$ is the new current flowing through the main circuit, hence the current flowing through $R$.
In the half deflection method, the value of S is adjusted such that the deflection is half of the original value when the key ${K_2}$ was not closed.
Thus,
$I{'_G} = \dfrac{{k\theta }}{2}$.
$\Rightarrow \dfrac{S}{{S + G}}I = \dfrac{{k\theta }}{2}$
Dividing equation above by $\dfrac{S}{{S + G}}I = \dfrac{{k\theta }}{2}$, and simplifying, we have
$\dfrac{{SI(R + G)}}{{E(S + G)}} = \dfrac{1}{2}$
Now, the equivalent resistance of the circuit is
${R_{eq}} = R + \dfrac{{SG}}{{S + G}}$. Then the current would be
$I = \dfrac{E}{{{R_{eq}}}} = \dfrac{E}{{R + \dfrac{{SG}}{{S + G}}}}$
Then substituting into $\dfrac{{SI(R + G)}}{{E(S + G)}} = \dfrac{1}{2}$ and then simplifying to make $G$ subject, we have
$G = \dfrac{{RS}}{{R - S}}$