Question
Question: In an experiment, the resistance of a material is plotted as a function of temperature (in some rang...
In an experiment, the resistance of a material is plotted as a function of temperature (in some range). As shown in the figure, it is a straight line. One may conclude that:
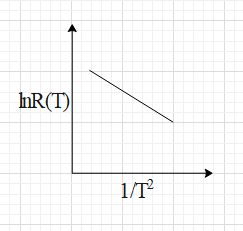
A. R(T)=T2T0
B. R(T)=R0eT02−T2
C. R(T)=R0eT2−T02
D. R(T)=R0eT02T2
Solution
Let us define some values of the temperature and resistance to help us in our calculations. Also we can see some extra terms or variables used in the options. check for which one we get a negative slope and positive constant.
Complete step by step answer:
In the given graph we can see that the x-axis represents a function of temperature T , i.e. T21 and the y-axis represents a function of resistance R, i.e. lnR.
The given graph represents a straight line and we know that the equation of a straight line can be written in the form y=mx+c …... (i).
In this case, y=lnR and x=T021.
m is the slope of the line and c is the y intercept.
Let x coordinate T21=0, the y coordinate be lnR0. This means that the y intercept of the line is c=lnR0.
Let y coordinate lnR=0, the x coordinate be T021. This means that the x intercept of the line is x=T021.
This can be depicted in the graph shown below.
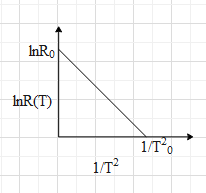
From the figure we get that slope m=0−T021lnR0−0=−T02lnR0.
Substitute the values of x, y, m and c in equation (i).
⇒lnR=(−T02lnR0)T21+lnR0
⇒lnR=lnR0(1−T2T02)
⇒elnR=elnR0(1−T2T02)
⇒R=elnR0.e(1−T2T02)
⇒R=R0e(1−T2T02)
⇒R=(R0e)e(T2−T02)
So, the correct answer is “Option C”.
Note:
Note that the constant that we defined and the constants used in the options are not the same. Therefore, it is not necessary that the equation in the solution and the option must be the same.
We can also check the correct option by the log to the base e on both sides of each and write in the form of the equation of a straight line. Then check for which one we get a negative slope and positive constant.
