Question

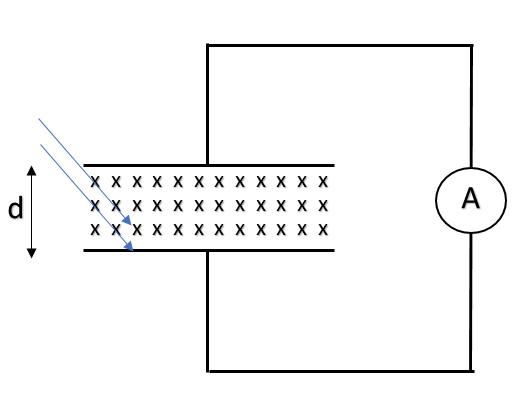
In an experiment on photoelectric effect, the emitter and the collector plates are placed at a separation ‘d’ and are connected through an ammeter without any cell. A magnetic field B exists parallel to the plane. The work function of the emitter is $\phi$ and light incident on it has wavelength $\lambda$. Then the minimum value of B for which ammeter register zero current will be (take mass of electron as ‘m’ and charge on it is ‘e’):

$\text{A.}\quad B = \dfrac{1}{2d}\sqrt{m\left(\dfrac{hc}{\lambda} - {\phi}\right)}$
$\text{B.}\quad B = \dfrac{2}{ed}\sqrt{2m\left(\dfrac{hc}{\lambda} - {\phi}\right)}$
$\text{C.}\quad B = \dfrac{1}{ed}\sqrt{m\left(\dfrac{hc}{\lambda} - {\dfrac{\phi}{2} }\right)}$
$\text{D.}\quad B = \dfrac{2}{ed}\sqrt{m\left(2\dfrac{hc}{\lambda} - {\phi}\right)}$

Answer 1

Different material has different values of work function and stopping potential. It is the property of the material which defines how much energy is needed to eject an electron from the surface of a metal. For example, ejecting electrons out is easiest in metals such as tungsten. The value of current to be zero in the ammeter, there should be no current in the circuit and hence no electron should reach from emitter to the opposite plate.

Formula used:
$\dfrac{hc}{\lambda} = \phi + \dfrac12 mv^2$, $r = \dfrac{mv}{Be}$

Complete answer:
Let’s first discuss the core concepts behind the problem. When we can say that there is no current in the circuit? It is when we can say that no current is flowing in the circuit. In other words, it is when all the electrons generated from the emitter get deviated by some means and could not reach the other plate of the capacitor shown. In this problem, it is the magnetic field which will deviate the electron from getting to the other plate.
Now, the velocity with which the electron will be ejected is given by:
$\dfrac{hc}{\lambda} = \phi + \dfrac12 mv^2$
$\implies v = \sqrt{\dfrac{2hc}{m\lambda} - \dfrac{2\phi}{m}}$
Now, since the magnetic field is perpendicular to the direction of motion, thus the path of the electron will be circular. And in order to get deviated before reaching the opposite plate, the electron has to travel in such a way that the diameter of the electron path is just equal to the separation between the plates.
Thus $r=\dfrac{d}{2}$
So using:
$r = \dfrac{mv}{Be}$
$v = \sqrt{\dfrac{2hc}{m\lambda} - \dfrac{2\phi}{m}}$
$\Rightarrow \dfrac d2 = \dfrac{m}{Be}\sqrt{\dfrac{2hc}{m\lambda} - \dfrac{2\phi}{m}}$
$\Rightarrow B = \dfrac{2m}{de}\sqrt{\dfrac{2hc}{m\lambda} - \dfrac{2\phi}{m}}$
$\therefore B = \dfrac{2}{ed}\sqrt{2m\left(\dfrac{hc}{\lambda} - {\phi}\right)}$

So, the correct answer is “Option B”.

Note:
These types of long statement questions are meant for confusion creation among students. But students must always follow the basics like here we’ve discussed “when there won’t be any current flowing through the circuit and why no electron will reach the other plate”. Also, one might think that it is not necessary that the electron will be ejected in an exact direction perpendicular to the field. Yes, that’s true but we are doing calculations so that the most energetic electron with the same direction can’t reach the other plate.