Question

In an examination, 30% and 35% of students respectively failed in history and geography while 27% of students failed in both the subjects. If the number of students passing the examination is 248, then find the total number of students who appeared in the examination.
A. 425
B. 400
C. 380
D. 725

Answer 1

We here have been given the percentage of students, which failed history and geography and also the percentage of students who failed both. Then we have been given the total number of students who passed the examination and we have been asked to find the total number of students who appeared in the examination. For this, we will first find the percentage of students who failed the examination. For this, we will use the formula from set theory given as $n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)$ where we will assume set A to be the set of students who failed history and B to be the set of students who failed geography. After that, we will find the percentage of students that passed by subtracting the percentage of students that failed from 100, and then we will assume the total number of students who gave the examination to be ‘x’. Then we will keep that percentage of x equal to the given number of students and hence we will form an equation. On solving that equation we will find the value of x and hence our required answer.

Complete step-by-step solution
We have been given that 30% of students failed in history and 35% of the students failed in geography and the percentage of students who failed in both the subjects is given to us 27%.
Thus, we first need to find the total percentage of students who failed.
We know that $n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)$
Here, if we consider:
Set A= set of students who failed history
Set B= set of students who failed geography
Then,
Set $A\cup B$= set of students who failed both the subjects
Set $A\cap B$= set of students who failed
Hence, we have:
$\begin{aligned} & n\left( A \right)=30\% \\\ & n\left( B \right)=35\% \\\ & n\left( A\cap B \right)=27\% \\\ \end{aligned}$
Thus, we get the percentage of students who failed the examination are:
$\begin{aligned} & n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right) \\\ & \Rightarrow n\left( A\cup B \right)=30+35-27 \\\ & \Rightarrow n\left( A\cup B \right)=65-27 \\\ & \Rightarrow n\left( A\cup B \right)=38\% \\\ \end{aligned}$
Hence, the percentage of students who failed the examination are 38%.
Thus, the percentage of students who passed the examination will be:
$\begin{aligned} & \left( 100-38 \right)\% \\\ & \Rightarrow 62\% \\\ \end{aligned}$
Hence, there are 62% students who passed the examination.
Now, we have been given that a total of 248 students passed the examination.
Now, let us assume the total number of students to be ‘x’. Thus, we can say that 62% of ‘x’ students passed the examination.
Hence, we can say that:
$\dfrac{62}{100}\times x=248$
Thus, solving for ‘x’, we get:
$\begin{aligned} & \dfrac{62}{100}\times x=248 \\\ & \Rightarrow \dfrac{62x}{100}=248 \\\ & \Rightarrow x=248\times \dfrac{100}{62} \\\ & \therefore x=400 \\\ \end{aligned}$
Thus, the total number of students in the examination are 400.
Hence, option (B) is the correct option.

Note: Here we have used the concept of set theory. Some few formulas for set theory are given as follows:
1. $n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)$

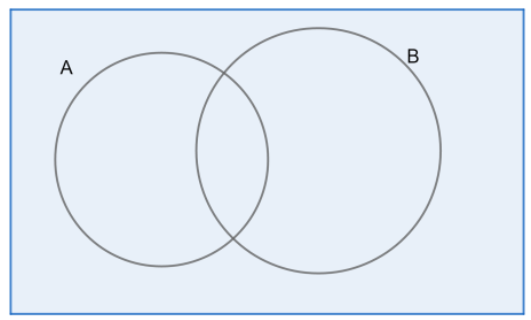
Here, we can see that when we add the elements of set A and B, the common area, i.e. $A\cap B$ is counted twice. Thus, we have subtracted it once.
2. $n\left( A\cup B\cup C \right)=n\left( A \right)+n\left( B \right)+n\left( C \right)-n\left( A\cap B \right)-n\left( B\cap C \right)-n\left( C\cap A \right)+n\left( A\cap B\cap C \right)$

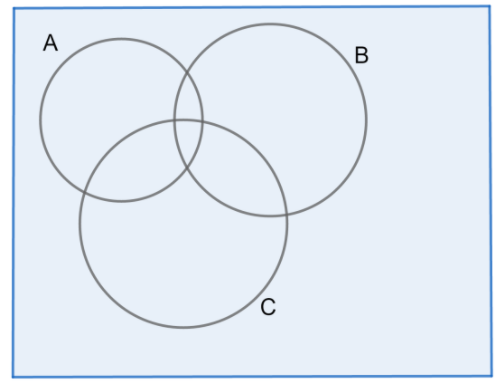
Here, we can see that when we add the elements of set A, B, and C, the elements common to set A and B, B and C, and A and C are counted twice so we subtract them. Due to this the area common to all of them is subtracted completely so it is added once again.
3. $n\left( {\bar{A}} \right)=n\left( U \right)-n\left( A \right)$

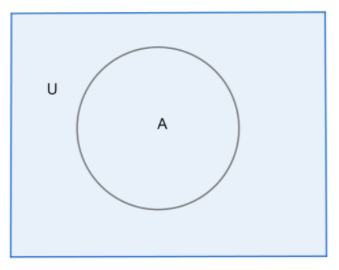
Here, to calculate the number of elements that do to belong to set A, we will subtract the number of elements inset A from the total number of elements, i.e. the number of elements in universal set U.