Question

In an exam 12% candidates failed in Physics, 10% candidates failed in math, 6% failed in both. If the total candidates who passed in physics only is 100 then, how many students gave the exam?

Answer 1

We assume the total number of students who gave the exam as a variable and using the concept of percentage we write the number of students who failed in physics, math and both physics and math. Subtract the number of students who failed in both physics and math from the number of students who failed in math to get the number of students who passed in physics only and form an equation using the given number in the question.

• $m\%$ of x can be written as $\dfrac{m}{{100}}x$

Complete step-by-step answer:
Let us assume total number of students who gave the exam as x
Now we are given 12% candidates failed in Physics, 10% candidates failed in math, 6% failed in both.
Let us assume A as students who failed in physics and B as students who failed in math.
Then using the concept of set theory we can draw a Venn diagram for the question.

Students who failed in physics is given by $n(A)$
Students who failed in math is given by $n(B)$
Students who failed in both physics and math is given by $n(A \cap B)$
We are given exam 12% candidates failed in Physics
Then from formula of percentage we can write
$\Rightarrow n(A) = \dfrac{{12}}{{100}}x$
Also, 10% candidates failed in math
Then from formula of percentage we can write
$\Rightarrow n(B) = \dfrac{{10}}{{100}}x$
And 6% failed in both physics and math
Then from formula of percentage we can write
$\Rightarrow n(A \cap B) = \dfrac{6}{{100}}x$
Now we form an equation from the statement given in the question.
We are given that the number of students who passed in physics only is 100.
Number of students who passed in physics only will be the number of students who failed in math only.
$\Rightarrow$The number of students who passed in physics only$=$number of students who failed in math$-$number of students who failed in both physics and math
Substitute the value of number of students who failed in math as $n(B)$and number of students who failed in both math and physics as $n(A \cap B)$
$\Rightarrow$The number of students who passed in physics only$= n(B) - n(A \cap B)$
Substitute the value of $n(B) = \dfrac{{10}}{{100}}x$and$n(A \cap B) = \dfrac{6}{{100}}x$
$\Rightarrow$The number of students who passed in physics only$= \dfrac{{10x}}{{100}} - \dfrac{{6x}}{{100}}$
$\Rightarrow$The number of students who passed in physics only$= \dfrac{{4x}}{{100}}$
Now equate the number of students who pass in physics only to 100.
$\Rightarrow \dfrac{{4x}}{{100}} = 100$
Cross multiply the denominator of LHS to RHS
$\Rightarrow 4x = 100 \times 100$
Divide both sides of the equation by 4
$\Rightarrow \dfrac{{4x}}{4} = \dfrac{{100 \times 100}}{4}$
Cancel same factors from numerator and denominator on both sides of the equation
$\Rightarrow x = 25 \times 100$
$\Rightarrow x = 2500$

So, the total number of students is 2500.

Note: Students might get confused in writing the equation for the number of students who passed in physics only. You can take help of the Venn diagram and use shading the area of respective fields to find the equation,

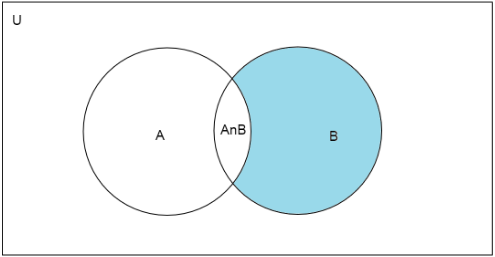
The blue shaded area shows students who passed in physics only.