Solveeit Logo
Login

Question

Question: In an ellipse, with center at the origin, if the difference of the length of the major axis and mino...

In an ellipse, with center at the origin, if the difference of the length of the major axis and minor axis is 10 and one of the foci at (0,53)\left( 0,5\sqrt{3} \right), then the length of the rectum is :
(a) 10
(b) 8
(c) 5
(d) 6

Explanation

Solution

Let us consider equation of the ellipse bex2a2+y2b2=1\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1. Then 2b−2a=102b-2a=10, where 2b is the length of the major axis and 2a is the length of the minor axis. be=53be=5\sqrt{3} , e is the eccentricity, (b > a). Use b2−a2=be2{{b}^{2}}-{{a}^{2}}={{be}^{2}} to find the value of a and b. then length of latus rectum =2a2b\dfrac{2{{a}^{2}}}{b}.

Complete step by step answer:
Let us draw a picture of the ellipse to understand the major axis, minor axis, latus rectum and origin of the ellipse.

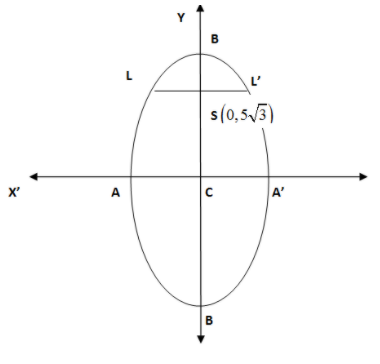
In this figure, we have BB′=2bBB'=2b is the length of major axis, AA′=2aAA'=2a is the length of minor axis, C is the origin of ellipse, and LSL’ is the length of latus rectum. S is the focus of the ellipse.
It is given that the difference between the length of the major axis and minor axis is 10.
∴2b−2a=10\therefore 2b-2a=10
⇒2(b−a)=10\Rightarrow 2\left( b-a \right)=10
⇒(b−a)=102\Rightarrow \left( b-a \right)=\dfrac{10}{2}
⇒(b−a)=5\Rightarrow \left( b-a \right)=5
Now, it is given that the focus is(0,53)\left( 0,5\sqrt{3} \right).
It means that,
be=53be=5\sqrt{3}
Squaring both sides, we get
⇒b2e2=(53)2\Rightarrow {{b}^{2}}{{e}^{2}}={{(5\sqrt{3})}^{2}}
⇒b2e2=75\Rightarrow {{b}^{2}}{{e}^{2}}=75
We know that
⇒e=1−a2b2\Rightarrow e=\sqrt{1-\dfrac{{{a}^{2}}}{{{b}^{2}}}}
\therefore $$$${{b}^{2}}{{\left( \sqrt{1-\dfrac{{{a}^{2}}}{{{b}^{2}}}} \right)}^{2}}=75 $$$$
⇒b2(1−a2b2)=75\Rightarrow {{b}^{2}}\left( 1-\dfrac{{{a}^{2}}}{{{b}^{2}}} \right)=75
⇒b2(b2−a2b2)=75\Rightarrow {{b}^{2}}\left( \dfrac{{{b}^{2}}-{{a}^{2}}}{{{b}^{2}}} \right)=75
⇒b2−a2=75\Rightarrow {{b}^{2}}-{{a}^{2}}=75
⇒(b−a)(b+a)=75\Rightarrow \left( b-a \right)\left( b+a \right)=75
From (1) we have,
b−a=5b-a=5
 ⇒5(b+a)=75~\Rightarrow 5\left( b+a \right)=75
⇒b+a=755\Rightarrow b+a=\dfrac{75}{5}
⇒b+a=15\Rightarrow b+a=15
Now we will solve equation (1) and (2). For this, add both equation (1) and (2).
b−a=5b-a=5
⇒b+a=15\Rightarrow b+a=15
We get,
⇒2b=20\Rightarrow 2b=20
⇒b=202\Rightarrow b=\dfrac{20}{2}
⇒b=10\Rightarrow b=10
Now we can find the value of a by putting b=10b=10either in equation (1) or (2).
Let us put b=10b=10in equation (1), then we have
⇒10−a=5\Rightarrow 10-a=5
⇒a=10−5\Rightarrow a=10-5
⇒a=5\Rightarrow a=5
Thus we have a=5a=5 andb=10b=10.
Now let us find the length of the latus rectum. We know that the length of the latus rectum =2a2b=\dfrac{2{{a}^{2}}}{b} .
Therefore, length of latus rectum =2(5)210=\dfrac{2{{\left( 5 \right)}^{2}}}{10}
=2×5×510=\dfrac{2\times 5\times 5}{10}
=5010=\dfrac{50}{10}
=5=5

So, the correct answer is “Option C”.

Note: The student must recognize whether b > a or a > b. According to this only, you can understand the length of major axis and minor axis. Also, you must keep in mind the length of latus rectum.