Question

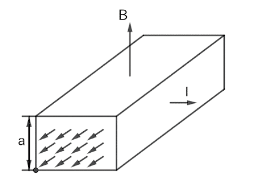
In an electromagnetic pump designed for transferring molten metals a pipe section with metal is located in a uniform magnetic field of induction $B$ (figure shown above). A current $I$ is made to flow across this pipe section in the direction perpendicular both to the vector $\vec{B}$ and to the axis of the pipe. The gauge pressure produced by the pump is $B=0.10T$ , $I=100A$ , and $a=2.0cm$ is $\dfrac{1}{x}kPa$ . Find $x$ .

Answer 1

Hint : For the pressure produced by the pump, we can calculate the area from the given dimensions and the force acts on the molten metal because it passes through a uniform magnetic field.

Complete Step By Step Answer:
Let us note down the given data;
Magnitude of the magnetic field $B=0.10T$
Current flowing through the cross section $I=100A$
Height of the section $a=2.0cm$
Length of the block perpendicular to the direction of magnetic field and parallel to the direction of current $l=?$
Gauge pressure produced by pump $P=\dfrac{1}{x}kPa$
For an object placed in a uniform magnetic field with its axis making an angle with the magnetic field, if a current is applied across the object in any direction, a force acts on the object which can be expressed as,
$\vec{F}=I(\vec{l}\times \vec{B})$
Here, for the given case, we are concerned with the magnitude of the force only, and the length of the object perpendicular to magnetic field, which is given by,
$F=IlB$
For the particular case, this force acting per unit area of the cross section is responsible for the gauge pressure.
The area of the cross section is given as,
$A=la$
Now, the gauge pressure is equal to the force acting per unit area, which is mathematically shown as,
$P=\dfrac{F}{A}$
Substituting the derived equations,
$\therefore P=\dfrac{IlB}{la}$
Canceling the common factor,
$\therefore P=\dfrac{IB}{a}$
Substituting the given values,
$\therefore P=\dfrac{100A\times 0.10T}{2.0cm}$
Converting the values to SI unit,
$\therefore P=\dfrac{100A\times 0.10T}{2.0\times {{10}^{-2}}m}$
Without considering the units,
$\therefore P=\dfrac{100\times 0.10}{2.0\times {{10}^{-2}}}$
Writing all the powers together,
$\therefore P=\dfrac{1}{2}\times {{10}^{2}}\times {{10}^{-1}}\times {{10}^{2}}$
$\therefore P=\dfrac{1}{2}\times {{10}^{3}}Pa$
We know that, $1kPa=1000Pa$
$\therefore P=\dfrac{1}{2}kPa$
Comparing this value with the given value, we get
$x=2$.

Note :
Here, the force acts on the object due to its orientation. If the object was arranged in such a way, that the length through which the current passes is parallel to the magnetic field, then no force acts on the object.