Question

In an electric circuit, the current passing through a conductor varies inversely with the resistance. Suppose that when the current is $17A$ (ampere), the resistance is $10ohms$. What is the resistance when the current is $5A$ ?

Answer 1

Using ohm's law, $V = I \times R$ where $V$ is voltage , $I$is the current and $R$ is the resistance in the circuit we will find $V$ , after that using the concept that the resistance will change appropriately if the voltage remains constant and the current changes we will find the resistance when the current is $5A$ .

Complete answer:
The Ohm's Law describes the relationship between current, voltage, and resistance in a circuit . The formula provides the answer.
$V = I \times R$ where I denote current (in ampere), V denotes voltage(in volts), and R denotes resistance (in ohms) in the circuit.
Putting the values of current and resistance in above, we get
$V = 17 \times 10$
Or , $V = 170volts$
Now, in a circuit if the voltage remains constant and current changes, the resistance will change proportionally. There is an inverse link between the two variables. If all other elements remain constant, the current drops as the resistance rises.

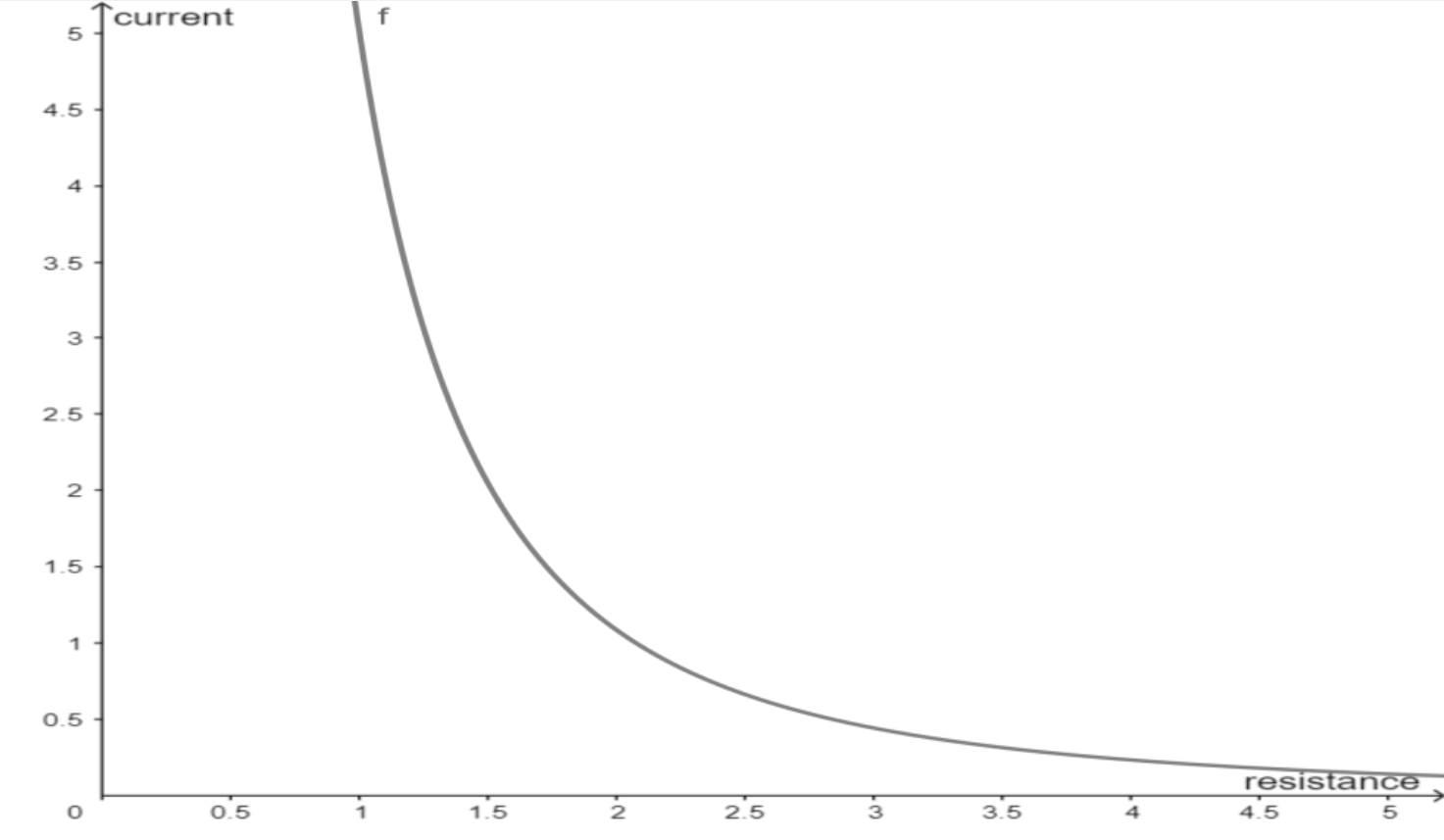
We can see the above graph between resistance and current . With an increase in resistance the current decreases . If the resistance is doubled, the current is cut in half; if the resistance is halved, the current is doubled.
$I \propto \dfrac{1}{R}$
In this case it will be $V = I \times R$
Therefore, $170 = 5 \times R$
$R = \dfrac{{170}}{5}$
$R = 34\Omega$
The resistance is $R = 34\Omega$ when current is $I = 5A$

Note: Another way of solving this question is
We use the relation between current and resistance that is $I \propto \dfrac{1}{R}$
Therefore we get, $\dfrac{{{I_1}}}{{{I_2}}} = \dfrac{{{R_2}}}{{{R_1}}}$
putting the values of current and resistance in above $\dfrac{{17}}{5} = \dfrac{R}{{10}}$
$R = 34ohms$
Which is the required solution.