Solveeit Logo
Login

Question

Question: In an aluminum (Al) bar of square cross section, a square hole is drilled and is filled with iron (F...

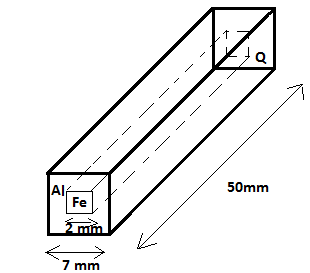
In an aluminum (Al) bar of square cross section, a square hole is drilled and is filled with iron (Fe) as shown in the figure. The electrical resistivity of Al and Fe are 2.7×10−8Ωm2.7\times {{10}^{-8}}\Omega m and 1.0×10−7Ωm1.0\times {{10}^{-7}}\Omega m, respectively. The electrical resistance between the two faces P and Q of the composite bar is

& A)\dfrac{2475}{64}\mu \Omega \\\ & B)\dfrac{1875}{64}\mu \Omega \\\ & C)\dfrac{1875}{49}\mu \Omega \\\ & D)\dfrac{2475}{132}\mu \Omega \\\ \end{aligned}$$
Explanation

Solution

Here, the resistance of aluminum and iron are in parallel connection. Hence, the formula for equivalent resistance in a parallel connection can be used here. But, here a small cross sectional area of aluminum is drilled and replaced with iron. Since the resistance depends on the cross sectional area of the object, resistance of the remaining aluminum will be the difference of area of aluminum and area of iron.

Formula used:
1Requivalent=1RAl+1Rfe\dfrac{1}{{{R}_{equivalent}}}=\dfrac{1}{{{R}_{Al}}}+\dfrac{1}{{{R}_{fe}}}
R=ρlAR=\rho \dfrac{l}{A}

Complete step by step answer:

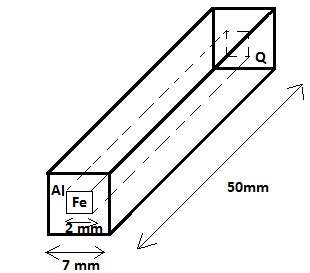
From the diagram we can see that, RAl{{R}_{Al}} and Rfe{{R}_{fe}} are parallel to each other.
Then, their equivalent resistance is given by,
1Requivalent=1RAl+1Rfe\dfrac{1}{{{R}_{equivalent}}}=\dfrac{1}{{{R}_{Al}}}+\dfrac{1}{{{R}_{fe}}}
We know,
Resistance,R=ρlAR=\rho \dfrac{l}{A}
Where,
ρ\rho is the resistivity of the material
ll is the length of the object
AA is the cross sectional area of the object
Given that,
Resistivity of aluminum, ρ1=2.7×10−8Ωm{{\rho }_{1}}=2.7\times {{10}^{-8}}\Omega m
Length of aluminum bar, l1=50mm{{l}_{1}}=50mm
Width of aluminum bar, w1=7mm{{w}_{1}}=7mm
Then, cross sectional area of aluminum, A1=7×10−3×7×10−3=49×10−6m2{{A}_{1}}=7\times {{10}^{-3}}\times 7\times {{10}^{-3}}=49\times {{10}^{-6}}{{m}^{2}}
Length of iron, l2=50mm{{l}_{2}}=50mm
Width of iron, w2=2mm{{w}_{2}}=2mm
Resistivity of iron, ρ2=1.0×10−7Ωm{{\rho }_{2}}=1.0\times {{10}^{-7}}\Omega m
Then, cross sectional area of iron, A2=2×10−3×2×10−3=4×10−6m2{{A}_{2}}=2\times {{10}^{-3}}\times 2\times {{10}^{-3}}=4\times {{10}^{-6}}{{m}^{2}}
Therefore, cross sectional area of the remaining aluminum,
A=A1−A2=49×10−6−4×10−6=45×10−6m2A={{A}_{1}}-{{A}_{2}}=49\times {{10}^{-6}}-4\times {{10}^{-6}}=45\times {{10}^{-6}}{{m}^{2}}
Then,
Resistance of aluminum, RAl=ρ1l1A=2.7×10−8×50×10−345×10−6=3×10−5Ω=30×10−6Ω{{R}_{Al}}={{\rho }_{1}}\dfrac{{{l}_{1}}}{A}=\dfrac{2.7\times {{10}^{-8}}\times 50\times {{10}^{-3}}}{45\times {{10}^{-6}}}=3\times {{10}^{-5}}\Omega =30\times {{10}^{-6}}\Omega

Resistance of iron, Rfe=ρ1l1A2=1.0×10−7×50×10−34×10−6=12.5×10−4Ω=1250×10−6Ω{{R}_{fe}}={{\rho }_{1}}\dfrac{{{l}_{1}}}{{{A}_{2}}}=\dfrac{1.0\times {{10}^{-7}}\times 50\times {{10}^{-3}}}{4\times {{10}^{-6}}}=12.5\times {{10}^{-4}}\Omega =1250\times {{10}^{-6}}\Omega
Therefore,
1Requivalent=1RAl+1Rfe=130×10−6+11250×10−6=1250×10−6+30×10−637500×10−12=1280×10−6375×10−12\dfrac{1}{{{R}_{equivalent}}}=\dfrac{1}{{{R}_{Al}}}+\dfrac{1}{{{R}_{fe}}}=\dfrac{1}{30\times {{10}^{-6}}}+\dfrac{1}{1250\times {{10}^{-6}}}=\dfrac{1250\times {{10}^{-6}}+30\times {{10}^{-6}}}{37500\times {{10}^{-12}}}=\dfrac{1280\times {{10}^{-6}}}{375\times {{10}^{-12}}}
1Requivalent=1280×10−637500×10−12\dfrac{1}{{{R}_{equivalent}}}=\dfrac{1280\times {{10}^{-6}}}{37500\times {{10}^{-12}}}
Then,
Requivalent=37500×10−121280×10−6=187564μΩ{{R}_{equivalent}}=\dfrac{37500\times {{10}^{-12}}}{1280\times {{10}^{-6}}}=\dfrac{1875}{64}\mu \Omega
The electrical resistance between the two faces P and Q of the composite bar is 187564μΩ\dfrac{1875}{64}\mu \Omega
Answer is option B.

Note:
Resistance of an object depends on its geometry and composition. Objects having large cross sectional areas have small resistance and objects with small cross sectional areas have high resistance. Different materials have different resistivity. And their resistivity depends only on temperature.