Question

In an aluminum (Al) bar of square cross section, a square hole is drilled and is filled with iron (Fe) as shown in the figure. The electrical resistivities of Al and Fe are $2.7\times {{10}^{-8}}\Omega m$ and $1.0\times {{10}^{-7}}\Omega m$, respectively. The electrical resistance between the two faces P and Q of the composite bar is

$\begin{aligned} & \text{A}\text{. }\dfrac{2475}{64}\mu \Omega \\\ & \text{B}\text{. }\dfrac{1875}{64}\mu \Omega \\\ & \text{C}\text{. }\dfrac{1875}{49}\mu \Omega \\\ & \text{D}\text{. }\dfrac{2475}{132}\mu \Omega \\\ \end{aligned}$

Answer 1

We have an iron bar in a square hole inside a square cross section of the aluminium bar. We need to find the electrical resistance between the two faces marked in the figure. By drawing the given 3 dimensional figure as a 2 dimensional figure and connecting it in a circuit we will get a better vision of the situation. Thus we can solve the question.

Formula used:
${{R}_{eff}}=\dfrac{{{R}_{1}}\times {{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$
$R=\dfrac{\rho l}{A}$

Complete step-by-step answer:
In the question we are given an aluminium bar of square cross section and it is said that a square hole is drilled in it and it is filled with iron.
From the figure we can see that the length of the square face of the aluminium rod is 7mm and of the iron rod is 2 mm. the side length of both are the same and is 50 mm.
We are also given the electrical resistivities of aluminium and iron as $2.7\times {{10}^{-8}}\Omega m$ and $1.0\times {{10}^{-7}}\Omega m$ respectively, i.e.
${{\rho }_{Al}}=2.7\times {{10}^{-8}}\Omega m$
${{\rho }_{Fe}}=1.0\times {{10}^{-7}}\Omega m$
We need to calculate the electrical resistance between the two faces marked as ‘P’ and ‘Q’ in the figure.
Let us view the given figure in 2D plane from one of the sides and connect it in an electrical circuit, it will appear as below.

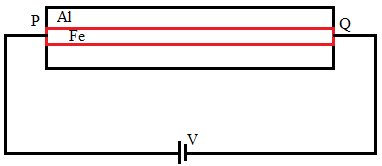
From this figure we can see that, when we connect it in an electrical circuit, they will be connected in parallel.
To find the electrical resistance between the faces P and Q, we need to find the electrical resistance in the circuit given above.
We know that for a circuit connected in parallel, the effective resistance is given by the formula,
${{R}_{eff}}=\dfrac{{{R}_{1}}\times {{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$, were ‘${{R}_{eff}}$’ is the effective resistance, ‘${{R}_{1}}$’ and ‘${{R}_{2}}$’ are the resistances of the resistors connected in the circuit.
Therefore in this case the effective resistance will be,
$\Rightarrow {{R}_{eff}}=\dfrac{{{R}_{Al}}\times {{R}_{Fe}}}{{{R}_{Al}}+{{R}_{Fe}}}$
We need to find the individual resistances of aluminium and iron.
We know that resistance and resistivity is related by the equation,
$R=\dfrac{\rho l}{A}$, were ‘$\rho$’ is the resistivity, ‘$l$’ is the length and ‘A’ is the area.
Therefore we can write the resistance of aluminium as,
$\Rightarrow {{R}_{Al}}=\dfrac{{{\rho }_{Al}}\times {{l}_{Al}}}{{{A}_{Al}}}$
We know that,
${{\rho }_{Al}}=2.7\times {{10}^{-8}}\Omega m$
Length of the aluminium bar, ${{l}_{Al}}=50mm=50\times {{10}^{-3}}m$
Area of the aluminium bar is the area subtracted from total area of the face P and area of the iron bar, i.e.
${{A}_{Al}}=A-{{A}_{Fe}}$
$\Rightarrow {{A}_{Al}}={{7}^{2}}-{{2}^{2}}m{{m}^{2}}$
$\Rightarrow {{A}_{Al}}=45m{{m}^{2}}=45\times {{10}^{-6}}{{m}^{2}}$
Therefore we get the resistance of the aluminum bar as,
$\Rightarrow {{R}_{Al}}=\dfrac{2.7\times {{10}^{-8}}\times 50\times {{10}^{-3}}}{45\times {{10}^{-6}}}$
$\Rightarrow {{R}_{Al}}=\dfrac{2.7\times {{10}^{-8}}\times 50}{45\times {{10}^{-3}}}$
$\Rightarrow {{R}_{Al}}=0.3\times {{10}^{-4}}\Omega$
Now we can write the resistance of iron bar as,
$\Rightarrow {{R}_{Fe}}=\dfrac{{{\rho }_{Fe}}\times {{l}_{Fe}}}{{{A}_{Fe}}}$
We have,
${{\rho }_{Fe}}=1.0\times {{10}^{-7}}\Omega m$
${{l}_{Fe}}=50mm=50\times {{10}^{-3}}m$
${{A}_{Fe}}=2\times 2m{{m}^{2}}$
$\Rightarrow {{A}_{Fe}}=4m{{m}^{2}}=4\times {{10}^{-6}}{{m}^{2}}$
Therefore we get the resistance of the iron bar as,
$\Rightarrow {{R}_{Fe}}=\dfrac{1.0\times {{10}^{-7}}\times 50\times {{10}^{-3}}}{4\times {{10}^{-6}}}$
$\Rightarrow {{R}_{Fe}}=\dfrac{1.0\times {{10}^{-7}}\times 50}{4\times {{10}^{-3}}}$
$\Rightarrow {{R}_{Fe}}=12.5\times {{10}^{-4}}\Omega$
Now that we have the individual resistances of iron and aluminium, we get the effective resistance as,
$\Rightarrow {{R}_{eff}}=\dfrac{\left( 0.3\times {{10}^{-4}} \right)\left( 12.5\times {{10}^{-4}} \right)}{\left( 0.3\times {{10}^{-4}}+12.5\times {{10}^{-4}} \right)}$
$\Rightarrow {{R}_{eff}}=\dfrac{0.3\times {{10}^{-4}}\times 12.5\times {{10}^{-4}}}{12.8\times {{10}^{-4}}}$
$\Rightarrow {{R}_{eff}}=\dfrac{0.3\times {{10}^{-4}}\times 12.5}{12.8}$
$\Rightarrow {{R}_{eff}}=\dfrac{1875}{64}\mu \Omega$
Therefore the electrical resistance between the faces P and Q is $\dfrac{1875}{64}\mu \Omega$.

So, the correct answer is “Option A”.

Note: Consider ‘n’ resistors connected as parallel in a circuit as shown in the figure below.

Let ${{R}_{1}},{{R}_{2}},.....{{R}_{n}}$ be the ‘n’ resistors connected as parallel.
Then the total resistance of the circuit were the resistors are connected in parallel is,
$\dfrac{1}{{{R}_{total}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}+....\dfrac{1}{{{R}_{n}}}$
If there are only two resistors in the system ‘${{R}_{1}}$’ and ‘${{R}_{2}}$’ then the total resistance will be,
$\dfrac{1}{{{R}_{total}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$
$\Rightarrow \dfrac{1}{{{R}_{total}}}=\dfrac{{{R}_{2}}+{{R}_{1}}}{{{R}_{1}}{{R}_{2}}}$
Therefore we get the total resistance of the circuit as,
$\Rightarrow {{R}_{total}}=\dfrac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$