Solveeit Logo
Login

Question

Question: In an AC circuit, the current lags behind the voltage by \[{\pi }/{3}\;\]. The components of the cir...

In an AC circuit, the current lags behind the voltage by π/3  {\pi }/{3}\;. The components of the circuit are:
A. R and L
B. L and C
C. R and C
D. Only R

Explanation

Solution

In a series L-R circuit, the current lags behind the voltage by a constant angle.

Complete step by step solution:
In a series L-R circuit, let an alternating emf E=Eosin⁡ωtE={{E}_{\text{o}}}\sin \omega t be applied to it.
Let i be the current in the circuit at any instant and VL{{V}_{L}} and VR{{V}_{R}} be the voltage across L and R respectively at that instant.
Then VL=iXL{{V}_{L}}=i{{X}_{L}} and VR=iR{{V}_{R}}=iR, where XL{{X}_{L}} is the inductive reactance. Now, VR{{V}_{R}} is in phase with the current i, while VL{{V}_{L}} leads i by 90o{{90}^{\text{o}}}.

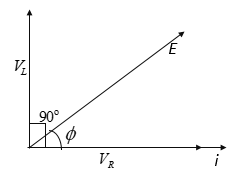
The phasor diagram above shows that , in L-R circuit, the voltage leads the current by a phase angle ϕ\phi is given by:

& \tan \phi =\dfrac{{{V}_{L}}}{{{V}_{R}}}=\dfrac{i{{X}_{L}}}{iR}=\dfrac{\omega L}{R} \\\ & \text{ }\phi ={{\tan }^{-1}}\dfrac{\omega L}{R} \\\ \end{aligned}$$ So, if in an AC circuit, the current lags behind the voltage by $${\pi }/{3}\;$$. The components of the circuit are L and R. **Therefore option A. is the correct answer.** **Additional information:** In a pure resistor circuit, the current is always in phase with the voltage. In a C-R circuit, the voltage lags behind the current by a constant angle. In a L-C circuit, the voltage across L leads the current in phase by $${{90}^{\text{o}}}$$, while the voltage across C lags behind the current in phase by $${{90}^{\text{o}}}$$. The phase difference between $${{V}_{L}}$$ and $${{V}_{C}}$$ is $${{180}^{\text{o}}}$$. **Note:** The inductor and resistance in a L-R circuit is connected in series. In the L-R circuit , $${{V}_{L}}$$ and $${{V}_{R}}$$ are mutually at right angles. Their sum is not equal to the impressed emf E. Form the equation of phase angle, it is clear that if $$L=0$$, then $$\phi =0$$(the emf and the current will be in the same phase); if $$R=0$$ then $$\phi ={{90}^{\text{o}}}$$(the emf will lead the current by $${{90}^{\text{o}}}$$).