Question

In an AC circuit $R=0\Omega$, ${{X}_{L}}=8\Omega$ & ${{X}_{C}}=6\Omega$ phase difference between voltage and current is :
A) ${{11}^{0}}$
B) ${{90}^{0}}$
C) ${{37}^{0}}$
D) ${{12}^{0}}$

Answer 1

The phase difference between voltage and current varies for RC and RC circuit. In resistors the phase difference between voltage and current are in phase. In RC the current leads the voltage and in the RC Current lags the voltage in the inductor we consider current whereas in capacitor we consider voltage.

Complete step-by-step solution:
when the capacitor or inductor are present in an AC circuit. The current and the voltage cannot peak at the same time the fraction of a period difference between the peaks expressed in degree is said to be the phase difference. In inductive circuits the current lags the voltage and in the capacitive circuit the current leads the voltage . Phasor diagram of $RLC$ circuit .

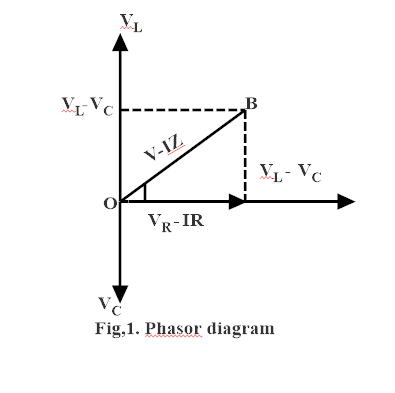
The phasor diagram of the $RLC$ series circuit when the circuit as an inductive circuit means$({{V}_{L}}>{{V}_{C}})$ is shown below and if $({{V}_{L}}<{{V}_{C}})$ the circuit will behave as a capacitive circuit
$V=\sqrt{{{V}_{R}}^{2}+{{({{V}_{L}}-{{V}_{C}})}^{2}}}$
$\phi ={{\tan }^{-1}}\dfrac{{{V}_{L}}-{{V}_{C}}}{{{V}_{R}}}$
$impedance(z)=\sqrt{{{R}^{2}}+{{({{X}_{L}}-{{X}_{C}})}^{2}}}$
$phase angle(\phi )={{\tan }^{-1}}\dfrac{{{X}_{L}}-{{X}_{C}}}{R}$ $\cdots \cdots (1)$
Power in $RLC$ series circuit is given by
$P=VI\cos \varphi$
Power factor is given by
$\cos \varphi =\dfrac{{{V}_{R}}}{V}$
In the question they have given the values of $R=0\Omega$ ${{X}_{L}}=8\Omega$ & ${{X}_{C}}=6\Omega$
Substitute in formula (1)
On substituting
$\phi ={{\tan }^{-1}}\dfrac{(8-6)}{0}$
$\phi ={{\tan }^{-1}}\dfrac{2}{0}$
$\phi =90$
So option B is correct.

Note: In a pure ohmic resistance, the current and voltage are both in phase as there is no phase difference between them. The current flows through the resistance is directly proportional to the voltage across it with this linear relationship in an AC circuit being called impedance and the indian standard frequency is 50Hz.