Question

In air, a charged soap bubble of radius 'r' is in equilibrium having outside and inside pressures equal. The charge on the bubble is ($\epsilon_0$ = permittivity of free space, T = surface tension of soap solution)

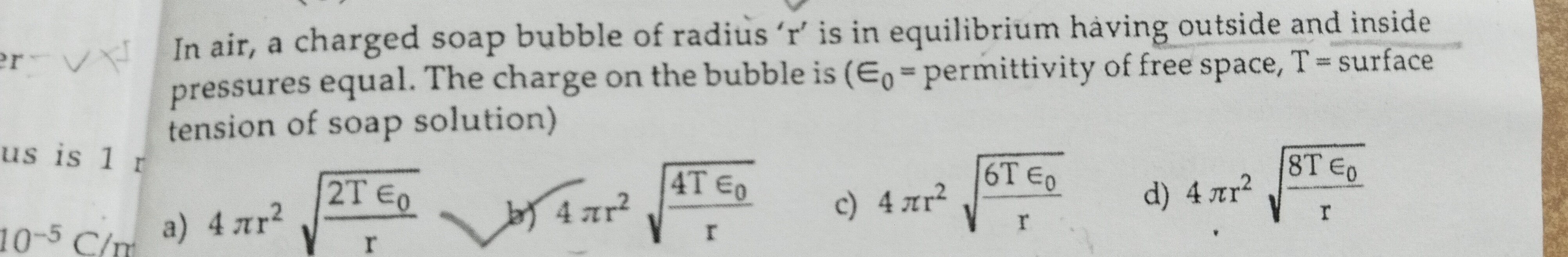
• A. $4\pi r^2 \sqrt{\frac{2T \epsilon_0}{r}}$
• B. $4\pi r^2 \sqrt{\frac{4T \epsilon_0}{r}}$
• C. $4\pi r^2 \sqrt{\frac{6T \epsilon_0}{r}}$
• D. $4\pi r^2 \sqrt{\frac{8T \epsilon_0}{r}}$

Answer 1

Answer: (D)

Option (d) $4\pi r^2 \sqrt{\frac{8T \epsilon_0}{r}}$

Answer 2

For a soap bubble, the Laplace pressure (excess pressure due to surface tension) is

$\Delta P = \frac{4T}{r}$.

A charged bubble develops an electric (Maxwell) pressure given by

$P_e = \frac{\sigma^2}{2\epsilon_0}$,

where the surface charge density is

$\sigma = \frac{Q}{4\pi r^2}$.

Thus,

$P_e = \frac{Q^2}{32\pi^2\epsilon_0 r^4}$.

For equilibrium (inside pressure equals outside pressure) this electric pressure must balance the Laplace pressure:

$\frac{Q^2}{32\pi^2\epsilon_0 r^4} = \frac{4T}{r}$.

Solve for $Q$:

$Q^2 = 32\pi^2\epsilon_0 r^4 \cdot \frac{4T}{r} = 128\pi^2\epsilon_0 T\, r^3$.

Taking the square root:

$Q = 8\pi \sqrt{2\epsilon_0 T\, r^3} = 4\pi r^2 \sqrt{\frac{8T\epsilon_0}{r}}$.