Question
Question: In air, a charged soap bubble of radius 'R' breaks into 27 small soap bubbles of equal radius 'r'. T...
In air, a charged soap bubble of radius 'R' breaks into 27 small soap bubbles of equal radius 'r'. Then the ratio of mechanical force acting per unit area of big soap bubble to that of a small soap bubble is
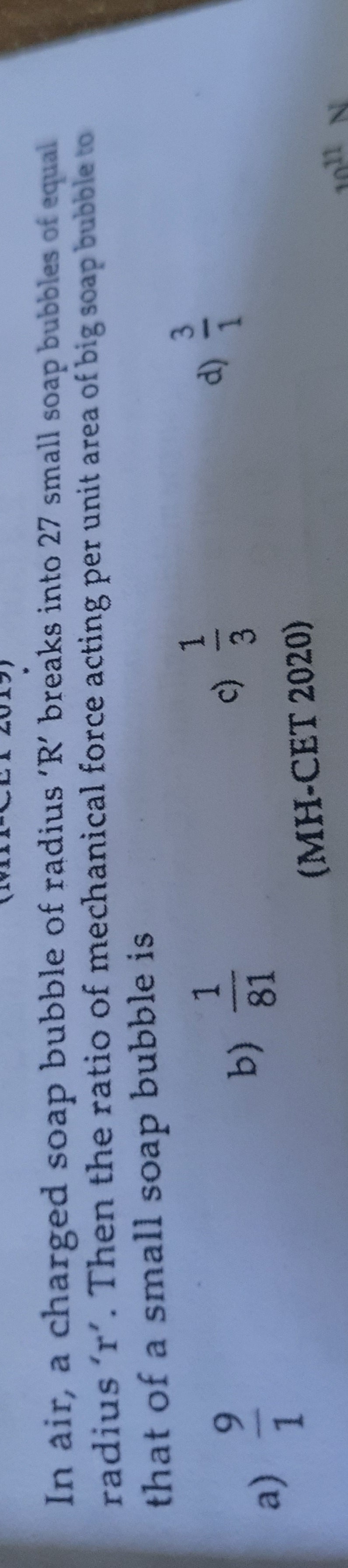
19
811
31
13
19
Solution
The problem involves understanding how the electrostatic pressure changes when a large charged soap bubble breaks into smaller ones. Here's a breakdown:
-
Volume Conservation:
The volume of the big bubble is Vbig=34πR3. The total volume of 27 small bubbles is 27×34πr3. Equating both volumes:
34πR3=27⋅34πr3⟹r3=27R3⟹r=3R -
Electrostatic Pressure (Force/Area):
For a charged conductor, the pressure due to surface charge density is given by P=2ϵ0σ2 with σ=4πR2Q. Thus, pressure on the big bubble is proportional to Pbig∝R4Q2.
When the bubble breaks, assuming charge is uniformly distributed, each small bubble gets charge q=27Q, and its pressure is proportional to:
Psmall∝r4q2=(3R)4(27Q)2=729Q2×R481=9R4Q2 -
Ratio of Pressures:
PsmallPbig=9R4Q2R4Q2=9
Thus, the ratio of mechanical force acting per unit area of the big bubble to that of a small bubble is 19.
