Question
Question: In above figure, a stick of length \(L = 1.85\,m\) oscillates as a physical pendulum. (a) What value...
In above figure, a stick of length L=1.85m oscillates as a physical pendulum. (a) What value of distance x between the stick's center of mass and pivot point O gives the least period? (b) What is the least period?
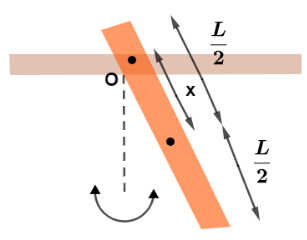
Solution
In order to solve this question we need to understand center of mass. Center of mass is a position of a system where all the mass can be concentrated and the system could be analyzed at one point. Here, we will use the general formula of time period for compound pendulum and using the concept of moment of inertia in different cases for a given situation of stick, we will determine the value of x and the least time period of stick.
Complete step by step answer:
Here the rod can be treated as a compound pendulum, so we apply the compound pendulum formula to get the time period of the rod.Let m be the mass of the rod and “l” be its length of rod.Also let the angular velocity of rod be ω.So from the compound pendulum formula we know, ω=Imgx. Here, I is the moment of inertia of rod about the pivot point and “x” is distance of COM from pivot point O.
(a) So the time period of rod is given as, T=ω2π
Putting values we get, T=2πmgxI
Since “I” is the moment of inertia of rod about pivot point O, so it is given from parallel axis theorem as, I=ICOM+Ix
Here, ICOM is the moment of inertia of rod about center of mass and it is given as, ICOM=12ml2
And Ix is the moment of inertia of rod due to length “x” of COM from pivot point O and is given as, Ix=mx2
Putting values we get, I=12ml2+mx2
Putting value of I in time period we get, T=2πmgxm(12l2+x2)
T=2π12gx(l2+12x2)→(i)
Now to minimize T we need to differentiate it w.r.t “x” and put it equal to zero, but it is difficult to differentiate T so we differentiate T2 in order to minimize T.
So T2=(2π)2(12g)2x2(l2+12x2)2
Let T2=P so P=(2π)2(12g)2x2(l2+12x2)2
So differentiating P with respect to “x” we get, dxdP=(12g)2(2π)2dxd(x2(l2+12x2)2
Using Differentiation rule of (vu)′=v2vu′−uv′ where u, v are the functions to be differentiated.
dxdP=(12g)2(2π)2[x4x2(24x)×2×(l2+12x2)−(l2+12x2)×2x]
⇒dxdP=(12g)2(2π)2x42x(l2+12x2)24x2−(l2+12x2)
⇒dxdP=(12g)2(2π)2x32(l2+12x2)12x2−l2
Now to minimize this function we need to put it equal to zero we get,
dxdP=0
Putting value we get,
(12g)2(2π)2x32(l2+12x2)12x2−l2=0
Since denominator and constant both cannot be zero so,
12x2−l2=0
⇒x2=12l2
⇒x=12l
⇒x=121.85
⇒x=0.53m
Therefore, the minimum value of “x” is, x=0.53m.
(b) we put the minimum value of “x” in equation (i) to get minimum value of T we get,
T=2π12(9.8)(0.53)(1.852+120.532)
Here, l=1.85m
x=0.53m And g=9.8ms−2
So time period is T=2π×0.3301sec
∴T=2.074sec
So minimum time period required is, T=2.074sec.
Note: It should be remembered that moment of inertia is defined as the product of mass and square of distance from the axis of rotation. And compound pendulums are such pendulums in which mass is distributed in length, surface area or volume of object. So here you see that center of mass is useful in identifying the locus of objects and its motion.
