Question
Question: In a Zener-regulated power supply a Zener diode with \({V_z} = 6\) volt is used for regulation. The ...
In a Zener-regulated power supply a Zener diode with Vz=6 volt is used for regulation. The load current is to be 4mA and the unregulated input is 10volt. What should be the value of the series resistor Rs, if the current through the diode is five-time the load current?
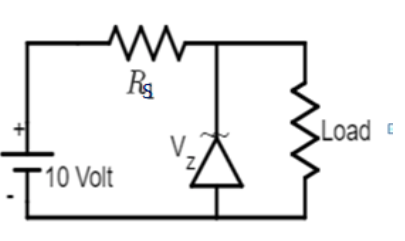
Solution
The total current (I) passing through the circuit is divided into two parts i.e. the current through Zener diode (Iz) and the current through the load (IL ).
∴I=Iz+IL .
Also, we have to find the voltage drop across the series resistance
Finally we get the series resistance by using the formula.
Formula used:
Total current, I=Iz+IL where Iz= the current through Zener diode, and IL= the current through the load.
The voltage drop across the series resistance RS, =Input voltage – Zener voltage.
Also, RS=Ivoltage−drop
Complete step by step answer:
In the given circuit system, an unregulated input voltage is connected in a side and a current is passing through the series resistance.
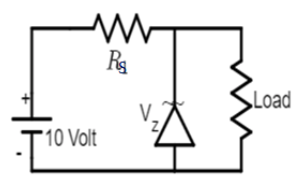
The total current (I) passing through the circuit is divided into two part i.e. the current through Zener diode (Iz) and the current through the load (IL) is as follows,
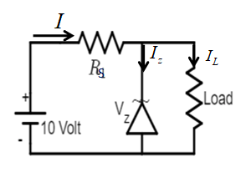
Here we can write it as ∴I=Iz+IL....(1)
Given the current through Zener diode (Iz) is 5 times the load current (IL) i.e. Iz=5IL.
It is given that the question , IL= 4mA and Iz=5IL....(2)
Putting the value IL in equation (2)we get,
⇒Iz=5×4mA
Let us multiply the term we get
⇒Iz=20mA
So, we have to find the total current on putting these values we get,
I=Iz+IL
⇒I=20+4
On adding the terms we get,
⇒I=24mA
⇒I=24×10−3mA
Now the voltage drop across the series resistance RS,
Input voltage – Zener voltage=10−6=4 volt.
Therefore the series resistance,
RS = Ivoltage - drop
Putting the values and we get
⇒RS=244
⇒RS=24×10−34Ω
On simplifying we get
⇒RS=166.66Ω
∴The value of the series resistor should be approx 167Ω .
Additional information:
-For the above circuit system, if the input unregulated voltage is changed increased or decreased, the current through the Zener diode is also changed in a direct manner (increased or decreased).
-Hence, the increased or decreased voltage drop across the series resistor does not affect the potential difference.
-This is because the break-down voltage is not increased due to an increase of the current through the Zener diode.
-This characteristic is used to make a circuit work as a voltage regulator.
Note: If the Rating of a Zener Diode is (Vz−Pz), the maximum safe current flow should be Imax=VzPz , where PZ is called watt rating, and VZ is called voltage rating of a diode.
In the mentioned circuit system the series resistor is chosen such as a value for which the Zener Current can not be greater than the maximum current (Imax ).
