Question

In a Young’s double slit experiment, the slit separation $d$ is $0.3mm$ and the screen distance $D$ is $1m$. A parallel beam of light of wavelength $600nm$ is incident on the slits at angle $\alpha$ as shown in the figure. On the screen, the point $O$ is equidistant from the slits and the distance $PO$ is $11.0mm$. Which of the following statement(s) is/are correct?

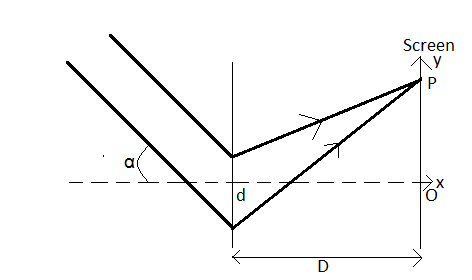
A) For $\alpha =0$, there will be constructive interference at point P.
B) For $\alpha =\dfrac{0.36}{\pi }$ degree, there will be destructive interference at point P.
C) For $\alpha =\dfrac{0.36}{\pi }$ degree, there will be destructive interference at point O.
D) Fringe spacing depends on $\alpha$

Answer 1

To solve this problem, we will find the total path difference in the two rays of light. The total path difference will be the sum of the path difference before entering the slits and the path difference after passing through the slit and reaching the screen. We will get a relation for the total path difference in terms of $\alpha$ and can hence, verify whether the options are correct.

Formula used:
$\Delta x=d\dfrac{y}{D}$
$\Delta x=n\lambda$
$\Delta x=\left( n+\dfrac{1}{2} \right)\lambda$

Complete step-by-step answer:
We will find the total path difference between the two rays of light as the sum of the path difference before entering the slits and after going through the slits and reaching the screen.
Hence, let us analyze the question.
The given slit separation is $d=0.3mm=0.3\times {{10}^{-3}}=3\times {{10}^{-4}}m$ $\left( \because 1mm={{10}^{-3}}m \right)$.
The separation between the slits and the screen is $D=1m$.
The distance $PO$ is $11mm=11\times {{10}^{-3}}m$ $\left( \because 1mm={{10}^{-3}}m \right)$.
The wavelength of the light used is $\lambda =600nm=600\times {{10}^{-9}}m=6\times {{10}^{-7}}m$ $\left( \because 1nm={{10}^{-9}}m \right)$.
Let the path difference developed between the light rays for the path before entering the slit be $\Delta {{x}_{1}}$.
Let the path difference between the light rays developed between the light rays for the path after passing through the slit and until reaching the screen be $\Delta {{x}_{2}}$.
Let the total path difference developed between the two light rays be $\Delta x$.

As explained above, the total path difference between the two rays of light is the sum of the path difference before entering the slits and after going through the slits and until reaching the screen.
$\therefore \Delta x=\Delta {{x}_{1}}+\Delta {{x}_{2}}$ --(1)
Now, we will attempt to find $\Delta {{x}_{1}}$ for which we will draw a more detailed diagram.

As we can see from the diagram, the path difference developed between the two rays before entering the slits is the length $SS'$.
By geometry, we see that
$SS'=d\sin \alpha$
$\therefore \Delta {{x}_{1}}=d\sin \alpha$
$\therefore \Delta {{x}_{1}}=d\alpha$ --(2) (Since for small $\alpha ,\sin \alpha \approx \alpha$)
Now, the path difference $x$ developed in the two light rays emerging from the light rays in a double slit experiment with distance between the slits as $d$ and separation between the slits and the screen as $D$ is given by
$x=d\dfrac{y}{D}$ --(3)
Where $y$ is the vertical distance of the point where the light rays meet on the screen from the midpoint of the separation of the two slits.
Using (3), we get
$\Delta {{x}_{2}}=d\dfrac{y}{D}$ --(4)
Using (1), (2) and (4), we get
$\Delta x=d\alpha +d\dfrac{y}{D}$ --(5)
Hence, we have got the total path difference developed in between the light rays.
Now, for constructive interference between two waves, the path difference $\Delta x$ is related to the wavelength $\lambda$ by
$\Delta x=n\lambda$
$\therefore \dfrac{\Delta x}{\lambda }=n$ --(6)
Where $\left( n=0,1,2,3.... \right)$
For destructive interference between two waves, the path difference $\Delta x$ is related to the wavelength $\lambda$ by
$\Delta x=\left( n+\dfrac{1}{2} \right)\lambda$
$\therefore \dfrac{\Delta x}{\lambda }=n+\dfrac{1}{2}$ --(7)
Where $\left( n=0,1,2,3.... \right)$
Therefore, now let us analyze the options.

(A) For $\alpha =0$, we get the path difference $\Delta x$, for the rays meeting at point P as
$\Delta x=d\left( 0 \right)+d\dfrac{y}{D}=d\dfrac{y}{D}$
For point $P$, $y=OP=11\times {{10}^{-3}}m$
$\therefore \Delta x=\left( 3\times {{10}^{-4}} \right)\dfrac{11\times {{10}^{-3}}}{1}=33\times {{10}^{-7}}m$
We divide the path difference by the wavelength and get
$\dfrac{\Delta x}{\lambda }=\dfrac{33\times {{10}^{-7}}}{6\times {{10}^{-7}}}=5.5=5+\dfrac{1}{2}$
Therefore, from (7), we get that there will be destructive interference.
Therefore option (A) is wrong.

(B) For $\alpha =\dfrac{0.36}{\pi }$degree, we get the path difference $\Delta x$, for the rays meeting at point P as
$\Delta x=d\left( \dfrac{0.36}{\pi }\times \dfrac{\pi }{180} \right)+d\dfrac{y}{D}=0.002d+d\dfrac{y}{D}$ $\left( \because 1rad=\dfrac{\pi }{180}\text{degree} \right)$
For point $P$, $y=OP=11\times {{10}^{-3}}m$
$\therefore \Delta x=\left( 0.002\times 3\times {{10}^{-4}} \right)+\left( \left( 3\times {{10}^{-4}} \right)\dfrac{11\times {{10}^{-3}}}{1} \right)=\left( 33+6 \right)\times {{10}^{-7}}m=39\times {{10}^{-7}}m$
We divide the path difference by the wavelength and get
$\dfrac{\Delta x}{\lambda }=\dfrac{39\times {{10}^{-7}}}{6\times {{10}^{-7}}}=6.5=6+\dfrac{1}{2}$
Therefore, from (7), we get that there will be destructive interference.
Therefore, option (B) is correct.

(C) For $\alpha =\dfrac{0.36}{\pi }$degree, we get the path difference $\Delta x$, for the rays meeting at point O as
$\Delta x=d\left( \dfrac{0.36}{\pi }\times \dfrac{\pi }{180} \right)+d\dfrac{y}{D}=0.002d+d\dfrac{y}{D}$ $\left( \because 1rad=\dfrac{\pi }{180}\text{degree} \right)$
For point O, $y=0$
$\therefore \Delta x=\left( 0.002\times 3\times {{10}^{-4}} \right)+\left( \left( 3\times {{10}^{-4}} \right)\dfrac{0}{1} \right)=\left( 6+0 \right)\times {{10}^{-7}}m=6\times {{10}^{-7}}m$
We divide the path difference by the wavelength and get
$\dfrac{\Delta x}{\lambda }=\dfrac{6\times {{10}^{-7}}}{6\times {{10}^{-7}}}=1$
Therefore, from (6), we get that there will be constructive interference.
Therefore, option (C) is wrong.

(D) Calculating the fringe width.
From (5), we get
$\Delta x=d\alpha +d\dfrac{y}{D}$
$\therefore d\dfrac{y}{D}=\Delta x-d\alpha$
$\therefore y=\dfrac{D}{d}\Delta x-d\alpha$ --(8)
Now let us find the fringe width by taking two successive bright fringes with positions $y'$ and $y''$ on the screen and respective path differences as $\Delta x'$ and $\Delta x''$.
Using (8), we get
$\therefore y'=\dfrac{D}{d}\Delta x'-d\alpha$ --(9)
$\therefore y''=\dfrac{D}{d}\Delta x''-d\alpha$ --(10)
For successive bright fringes,
$\Delta x''-\Delta x'=\left( n+1 \right)\lambda -n\lambda =\lambda \left( n+1-n \right)=\lambda \left( 1 \right)=\lambda$ --(11)
The fringe width $\beta$ is the difference in the vertical positions of two bright fringes.
$\therefore \beta =y''-y'$ --(12)
Putting (9) and (10) in (12), we get
$\beta =\dfrac{D}{d}\Delta x''-d\alpha -\left( \dfrac{D}{d}\Delta x'-d\alpha \right)=\dfrac{D}{d}\left( \Delta x''-\Delta x' \right)+\left( -d\alpha +d\alpha \right)=\dfrac{D}{d}\left( \Delta x''-\Delta x' \right)$
Putting (11) in the above equation, we get
$\beta =\dfrac{D}{d}\lambda$
Hence, we see that the fringe spacing does not depend on $\alpha$.
Therefore option (D) is wrong.
Therefore, the correct option is only (B).

Note: To solve such complex problems of the Young’s Double Slit Experiment, the best method to approach them is to draw a proper diagram and to find out the path difference between the rays of light that meet at the screen as a function of some variable. Often these relations can be found out by using simple geometry and trigonometry. Then by using the equations for the path difference, we can get required answers involving constructive and destructive interference.
Students should also be aware of the medium in which the apparatus is put. Since, the wavelength of light changes depending upon the medium in which the apparatus is put.