Question

In a Young’s double slit experiment, (slit distance d) monochromatic light of wavelength $\lambda$ is used and the figure pattern observed at a distance L from the slits. The angular position of the bright fringes is

& A.\,\,{{\sin }^{-1}}\left( \dfrac{N\lambda }{d} \right) \\\ & B.\,\,{{\sin }^{-1}}\left( \dfrac{\left( N+\dfrac{1}{2} \right)\lambda }{d} \right) \\\ & C.\,\,{{\sin }^{-1}}\left( \dfrac{N\lambda }{L} \right) \\\ & D.\,\,{{\sin }^{-1}}\left( \dfrac{\left( N+\dfrac{1}{2} \right)\lambda }{L} \right) \\\ \end{aligned}$$

Answer 1

We will make use of the path difference formula of the constructive interference to compute the value of the angular position of the bright fringes. Then, we will equate this equation with the product of the wavelength of the light and the order of diffraction.
Formulae used:
$\Delta =d\sin \theta$

Complete step-by-step solution:
From the given information, we have the data as follows.
In a Young’s double slit experiment, (slit distance d) monochromatic light of wavelength $\lambda$is used and the figure pattern observed at a distance L from the slits.
The formulae that we will be using to compute the angular position of the bright fringes is given as follows.
We will be using the path difference formula to compute the same. Considering the constructive interference, we have,
$\Delta =d\sin \theta$
Where $d$ is the slit distance and $\theta$ is the angle between the plane and the fringe (the angle of diffraction).
The diagram of YDSE

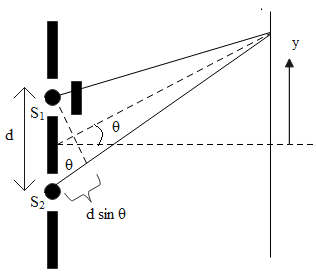
This value of the path difference equals the product of the wavelength of the monochromatic light and the order of diffraction.
$d\sin \theta =N\lambda$
Where $N$ is the order of diffraction and $\lambda$ is the wavelength of the monochromatic light.
Using this formula we will continue with the computation of the angular position of the bright fringes.
$\sin \theta =\dfrac{N\lambda }{d}$
Now multiply both the sides by the inverse sine function.
$\theta ={{\sin }^{-1}}\dfrac{N\lambda }{d}$
$\therefore$ The expression of the angular position of the bright fringes, is ${{\sin }^{-1}}\dfrac{N\lambda }{d}$, thus, the option (A) is correct.

Note: We have considered the constructive interference to compute the expression of the angular position of the bright fringes. The relation between the angle of diffraction and the wavelength of the monochromatic light should be known.