Solveeit Logo
Login

Question

Question: In a Wheatstone bridge, P=10\(\Omega \), Q=20\(\Omega \) , R= 30\(\Omega \).The value of S so that n...

In a Wheatstone bridge, P=10Ω\Omega , Q=20Ω\Omega , R= 30Ω\Omega .The value of S so that no current flows through the galvanometer:

Explanation

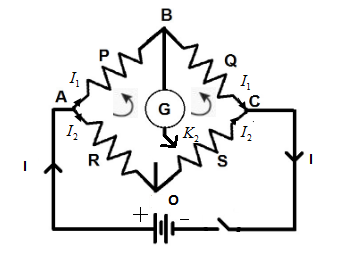
Solution

A Wheatstone Bridge is an electrical circuit used to measure an unknown resistance when the balanced condition of the two legs of the bridge circuit is satisfied. So when it is given that no current flows through the galvanometer, the balanced condition of the galvanometer must be satisfied. Following the balanced condition, the value of unknown resistance can be calculated.

Formula used:
PR=QS\dfrac{P}{R}=\dfrac{Q}{S} is the balanced condition of the Wheatstone bridge.
Where P, Q, R, S are the values of resistances.

Complete step by step answer:
A Wheatstone bridge circuit is given as follows:

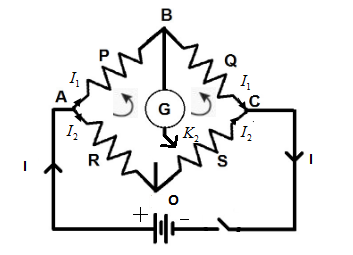
Fig: circuit diagram of wheatstone bridge where P, Q, R, S are the resistances and G is the galvanometer.
Given,
The value of resistors in the Bridge circuit
P=10 Ohm
Q=20 Ohm
R=30 Ohm
∵\because It is given that no current flows through the galvanometer of the wheatstone bridge circuit, it can be stated that the balanced condition of the wheatstone bridge is followed:
PR=QS\dfrac{P}{R}=\dfrac{Q}{S}
Plugging in the values of P, Q, R, we get the value of S as follows:
⇒1030=20S\Rightarrow \dfrac{10}{30}=\dfrac{20}{S}
⇒S=60Ω\Rightarrow S=60\Omega
Thus, we get the value of S as 60 Ohm when no current flows through the galvanometer.

Additional Information:
The balanced condition of the Wheatstone Bridge is given as follows in relation to the figure of the wheatstone Bridge:
AB=CD\dfrac{A}{B}=\dfrac{C}{D}

Where P, Q, R, S are the values of resistances in the bridge circuit.
When this condition is satisfied, no current passes through the galvanometer of the circuit. The condition is satisfied in the problem above, so we neglect the galvanometer from the circuit.

Note:
It is given that no current flows through the galvanometer so that the balanced condition is satisfied. In such a case, we can calculate the value of any unknown resistance of any of the given legs of the bridge since the potential difference across the arm AB is equal to the potential difference across the arm AO. Furthermore, the potential difference across BC is equal to that of CO. Conversely, if it is given that the balanced condition of the wheatstone bridge is satisfied, we can conclude that no current flows through the galvanometer.