Question

In a Wheat Stone’s network, $P = 2\Omega$ , $Q = 2\Omega$ , $R = 2\Omega$ and $S = 3\Omega$. The resistance with which $S$is to be shunted in order that the bridge may be balanced is:
A. $1\Omega$
B. $2\Omega$
C. $4\Omega$
D. $6\Omega$

Answer 1

We know that the Wheat Stone Bridge is said to be balanced when the ratio of resistances in the two arms is equal. Therefore, in this question we will first find the resistance $S'$ which is required to balance the bridge and then find the shunt resistance to be connected in parallel with $S = 3\Omega$ so that the resultant resistance will be equal to $S'$.

Complete step by step answer:
The Wheatstone Bridge will be balanced when the ratio of resistances in the two arms is equal. Let us consider the arrangement of wheatstone bridge as shown in figure where resistance $S'$ makes the wheatstone bridge balanced as shown in figure.

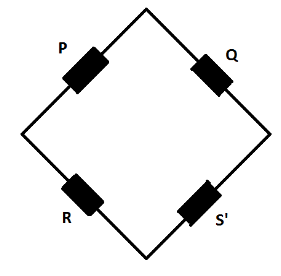
It is given in the question that $P = 2\Omega$ , $Q = 2\Omega$ and $R = 2\Omega$
For this Wheatstone bridge to be balanced the ratio of resistances in the two arms must be equal.
Therefore,

$$\dfrac{P}{Q} = \dfrac{R}{{S'}} \\\ \Rightarrow S' = \dfrac{{R \times Q}}{P} = \dfrac{{2 \times 2}}{2} = 2\Omega \\\$$

Thus the required resistance must be $2\Omega$ instead of $S = 3\Omega$ in order to make the Wheatstone bridge balanced. For this the shunt resistance $x$ must be connected in parallel with resistance $S = 3\Omega$to make the resultant resistance $2\Omega$ .

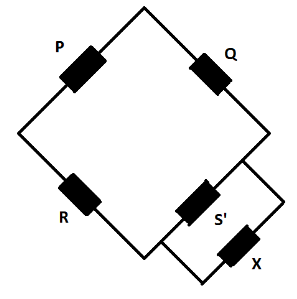
We know that for parallel connection,
\dfrac{1}{{S'}} = \dfrac{1}{S} + \dfrac{1}{x} \\\ \Rightarrow \dfrac{1}{x} = \dfrac{1}{{S'}} - \dfrac{1}{S} \\\ \Rightarrow \dfrac{1}{x} = \dfrac{1}{2} - \dfrac{1}{3} \\\ \Rightarrow \dfrac{1}{x} = \dfrac{1}{6} \\\ \therefore x = 6\Omega \\\
Thus, the resistance with which $S$is to be shunted in order that the bridge may be balanced is $6\Omega$ .

Hence, option D is the right answer.

Note: We know that wheat stone bridge is used to determine the unknown resistance as we have done in this problem. This is useful in many real life examples such as Wheatstone bridge along with an operational amplifier is used to measure physical parameters such as temperature, light, and strain. Also, Quantities such as impedance, inductance, and capacitance can be measured using variations on the Wheatstone bridge. The Wheatstone bridge is mainly used for the precise measurement of low resistance.