Question

In a village of 120 families, 93 families use firewood for cooking, 63 families use kerosene, 45 families use cooking gas, 45 families use firewood and kerosene, 24 families use kerosene and cooking gas, 27 families use cooking gas and firewood. Find how many use firewood, kerosene and cooking gas.
A. 10
B. 15
C. 20
D. 25

Answer 1

Hint : In this question, first draw the Venn diagram with the given data it will give us a clear picture of what we have to find out. Then the total number of families that use firewood, kerosene and cooking gas is given by their intersection of respective set of families. So, use this concept to reach the solution of the given problem.

Complete step by step solution :
Given the total number of families $n\left( U \right) = 120$
Let
The set of families use firewood $n\left( F \right) = 93$
The set of families use kerosene $n\left( K \right) = 63$
The set of families use cooking gas $n\left( G \right) = 45$
The set of families use firewood and kerosene $n\left( {F \cap K} \right) = 45$
The set of families use kerosene and cooking gas $n\left( {K \cap G} \right) = 24$
The set of families use cooking gas and kerosene $n\left( {G \cap F} \right) = 27$
Venn diagram for the above data is given in the below figure:

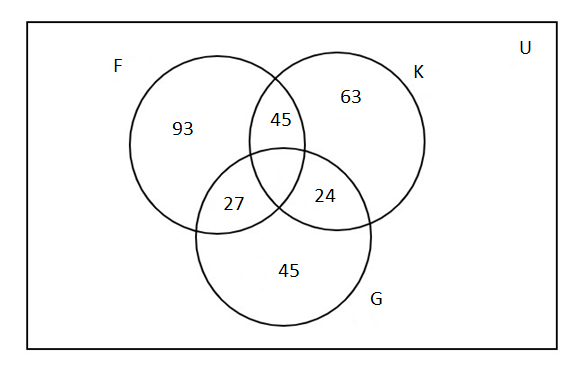
Clearly, from the diagram
The number of families who use firewood, kerosene and cooking gas is given by

\Rightarrow n\left( {F \cap K \cap G} \right) = n\left( U \right) - \left\\{ {n\left( F \right) + n\left( K \right) + n\left( G \right) - n\left( {F \cap K} \right) - n\left( {K \cap G} \right) - n\left( {G \cap F} \right)} \right\\} \\\ \Rightarrow n\left( {F \cap K \cap G} \right) = 120 - \left\\{ {93 + 63 + 45 - \left( {45 + 27 + 24} \right)} \right\\} \\\ \Rightarrow n\left( {F \cap K \cap G} \right) = 120 - 105 \\\ \therefore n\left( {F \cap K \cap G} \right) = 15 \\\

Thus, the correct option is B. 15

Note : The intersection of two sets $A$ and $B$, denoted by $A \cap B$, is the set containing all elements of $A$ that also belong to $B$ (or equivalently, all elements of $B$ that also belong to $A$). The union of two sets $A$ and $B$, denoted by $A \cup B$ is the set of all elements that are found in $A$ OR $B$(or both)