Question

In a vertical circle of radius (r), at what point in its path a particle may have tension equal to zero:
A. Highest point
B. lowest point
C. at any point
D. at a point horizontal from the centre of radius

Answer 1

So, at first by seeing the question we should be drawing the pictorial image of the question for easy understanding. Now analyze the force acting on the particle at each point then we can see that at the topmost position when the particle is attaining a certain velocity that it can complete one round of the circle without giving any force then the equation of tension will give the required result.

Complete step by step answer:

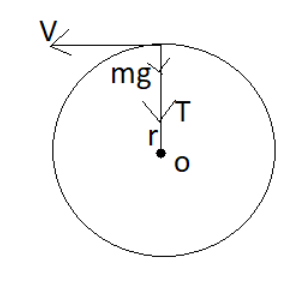
So, here in the diagram we see a string with which a particle is tied, V is shown the actual path of the particle if it is released and T is the tension in the string, mg is the weight of the particle that is acting vertically downwards at this position and r is the radius of the circle.
Now, we see that if the string was vertically downwards then this tension T would be working vertically upwards and the particle also experiences a centrifugal force.
Now, let’s see according to the question as the first option says that the tension in the string must be zero when the particle is vertically up at its highest point.
So, let us consider the tension of the string at the highest point be T.
Now we know that the minimum speed required by the particle at the heist point to complete the vertical circular motion is $v=\sqrt{gr}$.
So,
We can say that $\dfrac{m{{v}^{2}}}{r}=T+mg$
Or
$\dfrac{mgr}{r}=T+mg$,
So now on solving this we get T=0.

So, the correct answer is “Option A”.

Note: We, at first need to know how to draw a proper image for the given question or else this could not be solved. Now after drawing the image we have to analyze the tension of the string at each possible point to get the required result.