Question
Question: In a vector diagram shown In figure where \(\overrightarrow R \) is the resultant of vector \(\overr...
In a vector diagram shown In figure where R is the resultant of vector A and B . if R=2B , what is the value of angle θ?
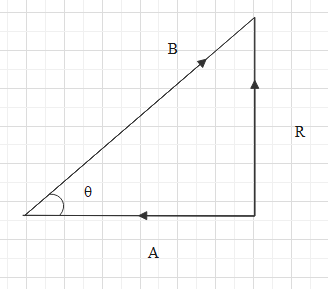
A.30θ
B.45θ
C.60θ
D.75θ
Solution
Hint- The resultant of two vectors A and B is denoted by R whose value is R=2B we need to find the angle made by these two vectors. This can be found by analysing the given figure. We know that sine of angle is given by the ratio of opposite sides by hypotenuse. Here, the opposite side is B and the adjacent side is R.
That is,
sinθ=BR
Using this we can find the angle θ .
Step by step solution:
It is given that two vectors A and B have a resultant vector R. The value of resultant vector is
given as ,
R=2B
We are asked to find the angle θ shown in the figure.
If we analyse the given triangle, we can see that the side opposite to the angle θ is R and the side adjacent is A and hypotenuse is B .
Therefore,
Adjacent side = A
Opposite side = R
Hypotenuse = B
We know that sine of an angle in a triangle can be calculated as the ratio of opposite sides to the hypotenuse .
sinθ=hypotenuseoppositeside
Substituting for opposite side and hypotenuse , we get
sinθ=BR …………..(1)
Now we need to find the value of BR .To find this value we can use the information given in the question. The value of R is given as R=2B . on rearranging this equation, we get
BR=21
Let us substitute this value in the equation (1). Then we get,
sinθ=21
We need to find the value of θ.
⇒θ=sin−121
We know that sin45∘=21 .
Therefore , sin−121=45∘
So,
θ=45∘
Hence the correct answer is option B.
Note: This question can also be done using an alternative method. The resultant vector A and Bis given by the equation.
R=A2+B2+2ABcosθ
On squaring and substituting value of R we get,
2B2=A2+B2+2ABcosθ ……………...(1)
Since A is perpendicular to R which is A+B we can write
On expanding the dot product we get, A2+ABcosθ=0
From this we get A=−Bcosθ. On substituting this value in equation 1 and solving for θ we get ,
θ=45∘
