Question

In a $\vartriangle ABC$, the values of a, c, A are given and ${b_1},{b_2}$ are two values of the third side b such that ${b_2} = 2{b_1}$. Then $\sin A =$ ?
A.$\sqrt {\dfrac{{9{a^2} - {c^2}}}{{8{a^2}}}}$
B. $\sqrt {\dfrac{{9{a^2} - {c^2}}}{{8{c^2}}}}$
C. $\sqrt {\dfrac{{9{a^2} + {c^2}}}{{8{a^2}}}}$
D. None of these

Answer 1

We use the law of cosines to calculate the cosine of angle A. Form a quadratic equation with variable ‘b’. Since ${b_1},{b_2}$ are two values of the third side b means that ${b_1},{b_2}$ are two roots of quadratic equation. Use the relation of roots with the coefficients of the equation to find the value of sine of angle A.

• In triangle ABC, if side a has opposite angle A, side b has opposite angle B and side c has opposite angle C then $\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$
• If a quadratic equation $a{x^2} + bx + c = 0$ has roots $\alpha ,\beta$ then we have relation between coefficients of equation and roots of equation as: $\alpha + \beta = \dfrac{{ - b}}{a}$ and $\alpha \beta = \dfrac{c}{a}$

Complete step by step solution:
We have a triangle ABC, sides opposite to angle A, B and C are a, b and c respectively.

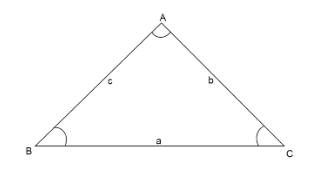
Use law of cosines
$\Rightarrow \cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$
Cross multiply the values
$\Rightarrow 2bc\cos A = {b^2} + {c^2} - {a^2}$
Shift all values to one side of the equation
$\Rightarrow {b^2} - 2bc\cos A + {c^2} - {a^2} = 0$
This forms a quadratic equation in ‘b’
$\Rightarrow {b^2} - \left( {2c\cos A} \right)b + \left( {{c^2} - {a^2}} \right) = 0$...............… (1)
Since it is given ${b_1},{b_2}$are two values of the third side b
Then ${b_1},{b_2}$are the roots of the equation (1)
Then we know ${b_1} + {b_2} = \dfrac{{ - ( - 2c\cos A)}}{1}$and${b_1}{b_2} = \dfrac{{{c^2} - {a^2}}}{1}$
I.e. ${b_1} + {b_2} = 2c\cos A$and${b_1}{b_2} = {c^2} - {a^2}$....................… (2)
Also, ${b_2} = 2{b_1}$
Substitute the value of ${b_2} = 2{b_1}$in ${b_1} + {b_2} = 2c\cos A$
$\Rightarrow {b_1} + 2{b_1} = 2c\cos A$
$\Rightarrow 3{b_1} = 2c\cos A$
Divide both sides by 3
$\Rightarrow {b_1} = \dfrac{{2c\cos A}}{3}$.................… (3)
Substitute the value of ${b_2} = 2{b_1}$in ${b_1}{b_2} = {c^2} - {a^2}$
$\Rightarrow {b_1} \times 2{b_1} = {c^2} - {a^2}$
$\Rightarrow 2{b_1}^2 = {c^2} - {a^2}$
Divide both sides by 2
$\Rightarrow {b_1}^2 = \dfrac{{{c^2} - {a^2}}}{2}$.............… (4)
Square equation (3) and equate it to equation (4)
$\Rightarrow {\left( {\dfrac{{2c\cos A}}{3}} \right)^2} = \dfrac{{{c^2} - {a^2}}}{2}$
Cross multiply the values
$\Rightarrow \dfrac{{2 \times 4{c^2}{{\cos }^2}A}}{9} = {c^2} - {a^2}$
$\Rightarrow \dfrac{{8{c^2}{{\cos }^2}A}}{9} = {c^2} - {a^2}$
Cross multiply the values
$\Rightarrow 8{c^2}{\cos ^2}A = 9{c^2} - 9{a^2}$
Divide both sides by $8{c^2}$
$\Rightarrow {\cos ^2}A = \dfrac{{9{c^2} - 9{a^2}}}{{8{c^2}}}$
Since we know ${\cos ^2}x = 1 - {\sin ^2}x$
$\Rightarrow 1 - {\sin ^2}A = \dfrac{{9{c^2} - 9{a^2}}}{{8{c^2}}}$
Shift all constant values to one side of the equation
$\Rightarrow 1 - \dfrac{{9{c^2} - 9{a^2}}}{{8{c^2}}} = {\sin ^2}A$
Take LCM in LHS
$\Rightarrow \dfrac{{8{c^2} - 9{c^2} + 9{a^2}}}{{8{c^2}}} = {\sin ^2}A$
$\Rightarrow \dfrac{{9{a^2} - {c^2}}}{{8{c^2}}} = {\sin ^2}A$
Take Square root on both sides of the equation
$\Rightarrow \sqrt {\dfrac{{9{a^2} - {c^2}}}{{8{c^2}}}} = \sqrt {{{\sin }^2}A}$
Cancel square root by square power
$\Rightarrow \sin A = \sqrt {\dfrac{{9{a^2} - {c^2}}}{{8{c^2}}}}$
$\therefore$The value of $\sin A$ is $\sqrt {\dfrac{{9{a^2} - {c^2}}}{{8{c^2}}}}$.

$\therefore$Correct option is B.

Note: Students are likely to make the mistake of assuming the variable in the quadratic equation as ‘c’ which is wrong because we are given the values of a, c and A are given. The question states the values of ‘b’ are ${b_1},{b_2}$ so the variable has to be ‘b’ in the quadratic equation then only we can find its roots.