Solveeit Logo
Login

Question

Question: In a unit cube. Find the angle between the diagonals of two faces of the cube through the same verte...

In a unit cube. Find the angle between the diagonals of two faces of the cube through the same vertex?

Explanation

Solution

To answer this question we have to consider a unit cube first and then we should consider any two faces with the same vertex and then draw the diagonals. we should find the vectors from the diagonals as we have the points forming the diagonals. From this we can consider the angles between them with the formula of angle between two vectors.

Complete step by step solution:
The given problem can be drawn in figure as shown below,

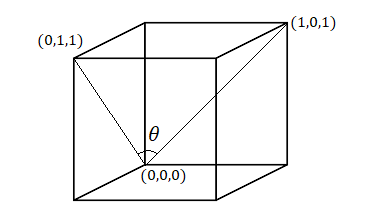
Let us consider two faces in the figure,
Now let us join the points (0,0,0) to (1,0,1) and (0,0,0) to (0,1,1)
Vector representations of the diagonals joining the points (0,0,0) to (1,0,1) is as below,
a⃗\vec{a} = \left( {{x}_{2}}-{{x}_{1}} \right)$$$$\hat{i} + \left( {{y}_{2}}-{{y}_{1}} \right)$$$$\hat{j} + \left( {{z}_{2}}-{{z}_{1}} \right)$$$$\hat{k}
⇒\Rightarrow \left( 1-0 \right)$$$$\hat{i} + \left( 0-0 \right)$$$$\hat{j} + \left( 1-0 \right)$$$$\hat{k}
⇒\Rightarrow i^\hat{i} + k^\hat{k}
So, ∣a⃗∣\left| {\vec{a}} \right| = 12+0+12=2\sqrt{{{1}^{2}}+0+{{1}^{2}}}=\sqrt{2}
Vector representations of the diagonals joining the points (0,0,0) to (0,1,1) is as below,
b⃗\vec{b} = \left( {{x}_{4}}-{{x}_{3}} \right)$$$$\hat{i} + \left( {{y}_{4}}-{{y}_{3}} \right)$$$$\hat{j} + \left( {{z}_{4}}-{{z}_{3}} \right)$$$$\hat{k}
⇒\Rightarrow \left( 0-0 \right)$$$$\hat{i} + \left( 1-0 \right)$$$$\hat{j} + \left( 1-0 \right)$$$$\hat{k}
⇒\Rightarrow j^\hat{j} + k^\hat{k}
So, ∣b⃗∣\left| {\vec{b}} \right| = 0+12+12=2\sqrt{0+{{1}^{2}}+{{1}^{2}}}=\sqrt{2}
Let θ be the angle between the two vectors.
We know, cos⁡θ=a⃗ . b⃗∣a⃗∣ ∣b⃗∣\cos \theta =\dfrac{\vec{a}\text{ }.\text{ }\vec{b}}{\left| {\vec{a}} \right|\text{ }\left| {\vec{b}} \right|}
cos⁡θ=(i⃗+k⃗).(j⃗+k⃗)2×2\cos \theta =\dfrac{\left( \vec{i}+\vec{k} \right).\left( \vec{j}+\vec{k} \right)}{\sqrt{2}\times \sqrt{2}}
cos⁡θ=12\cos \theta =\dfrac{1}{2}
θ=cos⁡−112\theta ={{\cos }^{-1}}\dfrac{1}{2}
=π3=\dfrac{\pi }{3}
So the angle required between the diagonals of two faces of the cube through the same vertex is given as π3\dfrac{\pi }{3}

Note: Students have to consider the unit cube as shown with the required diagonals as any mistake in this step can lead to wrong answers. The formula to find the angle between two vectors should be known to get the angles between the diagonals.