Question

In a triangle, the lengths of two larger sides are $10$ and $9$ respectively. If the angles are in A.P, the length of the third side can be? (Multiple correct choices)
A. $5 - \sqrt 6$
B. $3\sqrt 3$
C. $5$
D. $5 + \sqrt 6$

Answer 1

We first take the angles in general form of an AP and then use the property that the sum of three angles of a triangle is supplementary to find one angle. Then we apply the law of cosine on that angle and solve for the value of the third side.

• If one side of a triangle is longer than the other side of the triangle then the angle opposite to the longer side will be larger than the angle opposite to the shorter side.

Formula used:

• An arithmetic progression (A.P) is a sequence of numbers which always have the same difference between them. In an A.P with the first term $a$ and common difference $d$, we can write the ${n^{th}}$ term using the formula ${a_n} = a + (n - 1)d$, where ${a_n}$ is the ${n^{th}}$ term of A.P.
• Law of cosines states that if we are given lengths of two sides of a triangle and the angle between them, then we can find the length of the third side using the formula $\cos (A) = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$ where the $\vartriangle ABC$ has sides $AB = c,BC = a,CA = b$ opposite to angles $\angle C,\angle A,\angle B$ respectively.
  

Complete step-by-step answer:
Since we are given the lengths of two sides of a triangle in which one is larger than the other, we draw a triangle showing the sides of the triangle. Let the triangle be $\vartriangle ABC$.

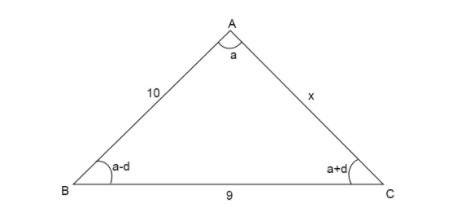
Here in $\vartriangle ABC$, the longest side is $AB = 10$, then the shorter side is $BC = 9$ and the shortest side is $AC$. Let us assume the length of side $AC = x$
We know the angles of $\vartriangle ABC$ are in A.P , therefore, they can be written in the form of an A.P where $a - d$ is the first term, then using the formula for the second and the third term we calculate

$${a_1} = a - d \\\ {a_2} = {a_1} + (2 - 1)d = a - d + d = a \\\ {a_3} = {a_1} + (3 - 1)d = a - d + 2d = a + d \\\$$

So, the angles in A.P are $a - d, a, a + d$. From the figure $\angle B = a - d,\angle A = a,\angle C = a + d$
Now, since $a + d$ is the largest angle, therefore it must be opposite to the longest side.
So, $\angle C$ is opposite to $AB = 10$
Second largest angle $a$ will be opposite to the second longest side.
So, $\angle A$ is opposite to $BC = 9$
Then the smallest angle $a - d$ will be opposite to the shortest side.
So, $\angle B$ is opposite to $AC = x$.
Now since we know the sum of all three angles of a triangle is equal to ${180^ \circ }$.
In $\vartriangle ABC$,
$\Rightarrow \angle A + \angle B + \angle C = {180^ \circ }$
Substituting the values of $\angle B = a - d,\angle A = a,\angle C = a + d$, we get

$$(a) + (a - d) + (a + d) = {180^ \circ } \\\ a + a - d + a + d = {180^ \circ } \\\ 3a = {180^ \circ } \\\$$

Dividing both sides of the equation by $3$

$$\dfrac{{3a}}{3} = \dfrac{{{{180}^ \circ }}}{3} \\\ a = {60^ \circ } \\\$$

Therefore, $\angle A = {60^ \circ }$.
Now using this angle measure and the sides between which this angle lies, we can apply the law of cosines to find the third side.
We know according to law of cosines, $\cos (A) = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$ where the $\vartriangle ABC$ has sides $AB = c, BC = a, AC = b$ opposite to angles $\angle C,\angle A,\angle B$ respectively. Here on comparing the sides and the angles we see that
$\angle A = {60^ \circ }$ and $c = 10,a = 9,b = x$.
Substituting the values in the formula we get
$\Rightarrow \cos ({60^ \circ }) = \dfrac{{{x^2} + {{10}^2} - {9^2}}}{{2 \times x \times 10}}$
Since we know the value of $\cos ({60^ \circ }) = \dfrac{1}{2}$, therefore the equation becomes
$\Rightarrow \dfrac{1}{2} = \dfrac{{{x^2} + 100 - 81}}{{20x}}$
Cross multiplying the denominators of sides to the numerator of opposite sides,
$\Rightarrow 20x = ({x^2} + 19) \times 2$
Dividing both sides of the equation by two

$$\Rightarrow \dfrac{{20x}}{2} = ({x^2} + 19) \times \dfrac{2}{2} \\\ \Rightarrow 10x = {x^2} + 19 \\\$$

Shifting all the values to one side to make a quadratic equation
$\Rightarrow {x^2} - 10x + 19 = 0$
On comparing with general quadratic equation $a{x^2} + bx + c = 0,a = 1,b = - 10,c = 19$
To find roots of the quadratic equation we use the formula $x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$
Substituting the values in the formula we get

$$\Rightarrow x = \dfrac{{ - ( - 10) \pm \sqrt {{{( - 10)}^2} - 4(1)(19)} }}{{2(1)}} \\\ \Rightarrow x = \dfrac{{10 \pm \sqrt {100 - 76} }}{2} \\\ \Rightarrow x = \dfrac{{10 \pm \sqrt {24} }}{2} \\\$$

Breaking the value inside the square root as $24 = 4 \times 6$ and using the property $\sqrt {mn} = \sqrt m \times \sqrt n$

$$\Rightarrow x = \dfrac{{10 \pm \sqrt {4 \times 6} }}{2} \\\ \Rightarrow x = \dfrac{{10 \pm \sqrt 4 \times \sqrt 6 }}{2} \\\$$

Now we know $\sqrt 4 = \pm 2$
$\Rightarrow x = \dfrac{{10 \pm 2\sqrt 6 }}{2}$
Taking $2$ common from the values in the numerator and cancelling it by the same value in the denominator.

$$\Rightarrow x = \dfrac{{2(5 \pm \sqrt 6 )}}{2} \\\ \Rightarrow x = 5 \pm \sqrt 6 \\\$$

So, there are two values of the third side $5 + \sqrt 6 ,5 - \sqrt 6$

So, the correct answer is “Option A” and “Option D” .

Note: Students are likely to get confused while applying the law of cosines formula and write sides length in wrong manner in the numerator. Keep in mind the angle which lies between two sides is taken cosine of, and on RHS of the equation, numerator has sum of squares of two sides between which the angle lies and subtract square of side opposite to the angle and the denominator has twice the product of lines in between which the angle lies.