Solveeit Logo
Login

Question

Question: In a triangle ABC, using the vectors, prove that \({c^2} = {a^2} + {b^2} - 2ab\cos C\)....

In a triangle ABC, using the vectors, prove that c2=a2+b2−2abcos⁡C{c^2} = {a^2} + {b^2} - 2ab\cos C.

Explanation

Solution

Hint: Analyse the situation with a figure. The side with length a is the side opposite to angle C. Assume the sides representing vectors, use polygons law of vectors and then simplify it further to get the desired result.

Complete step by step answer:


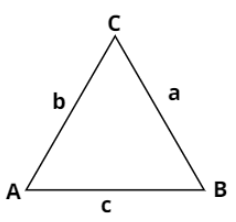
As we have ABC is a triangle then by using polygons law we can say that a⃗+b⃗+c⃗=0\vec a + \vec b + \vec c = 0
Then
a⃗+b⃗=−c⃗\vec a + \vec b = - \vec c
Now on squaring both sides, we get
⇒(a⃗+b⃗)(a⃗+b⃗)=(−c⃗)(−c⃗)\Rightarrow (\vec a + \vec b)(\vec a + \vec b) = ( - \vec c)( - \vec c)
On applying dot product rule on RHS term we get
⇒b2+a2+2abcos⁡(π−C)=c2\Rightarrow {b^2} + {a^2} + 2ab\cos (\pi - C) = {c^2}
⇒a2+b2+2ab(−cos⁡C)=c2\Rightarrow {a^2} + {b^2} + 2ab( - \cos C) = {c^2}
⇒c2=a2+b2−2abcos⁡C\Rightarrow {c^2} = {a^2} + {b^2} - 2ab\cos C

Hence we have proved that in a triangle ABCc2=a2+b2−2abcos⁡C{c^2} = {a^2} + {b^2} - 2ab\cos C.

NOTE: The polygon law used above states that if three vectors, a⃗,b⃗ and c⃗\vec a,\vec b{\text{ and }}\vec c are such that, a⃗+b⃗+c⃗=0\vec a + \vec b + \vec c = 0 then the vectors a⃗,b⃗ and c⃗\vec a,\vec b{\text{ and }}\vec c will form a triangle.