Question

In a triangle, ABC, the orthocentre and the circumcentre are at equal distances from the side BC and lie on the same side of BC, then tanBtanC is equal to
[a] 3
[b] $\dfrac{1}{3}$
[c] -3
[d] $\dfrac{-1}{3}$

Answer 1

Hint: Use the fact that the distance of the orthocentre from the side BC is given by d = 2RcosBcosC. Use the fact that the distance of the circumcentre from the side BC is given by RcosA. Equate the two distances and use the fact that in a triangle ABC, $A+B+C=\pi$. Use the property $\cos \left( x+y \right)=\cos x\cos y-\sin x\sin y$ and hence find the value of $\tan B\tan C$

Complete step-by-step answer:

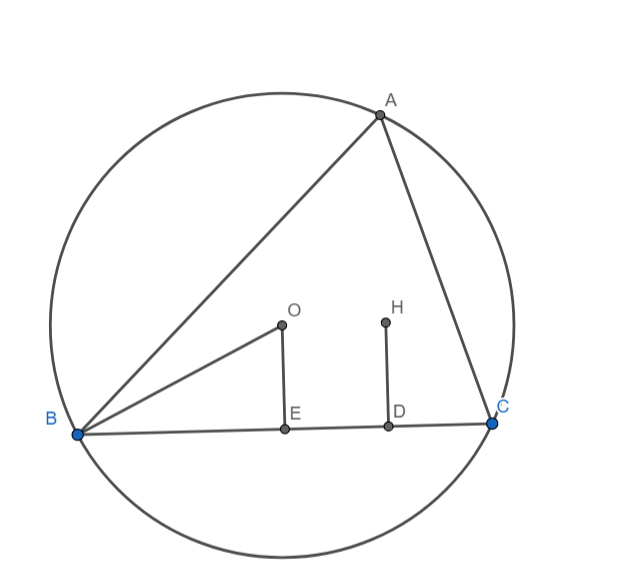
Given: ABC is a triangle, O the circumcentre of the triangle and H is the orthocentre of the triangle. OE is the distance of O from BC and HD is the distance of H from BC. OE = HD
To determine: The value of tanBtanC
We know that the distance of the circumcentre from the side BC is given by $d=R\cos A$
Hence, we have
$OE=R\cos A$
We know that the distance of the circumcentre from the side BC is given by $d=2R\cos B\cos V$
Hence, we have
$HD=2R\cos B\cos C$
But Given that OE = HD
Hence, we have
$R\cos A=2R\cos B\cos C$
Dividing both sides by R, we get
$\cos A=2\cos B\cos C$
Now, we know that by angle sum property of a triangle $A+B+C=\pi$
Subtracting B+C from both sides, we get
$A=\pi -\left( B+C \right)$
Hence, we have
$\cos \left( \pi -\left( B+C \right) \right)=2\cos B\cos C$
We know that $\cos \left( \pi -x \right)=-\cos x$
Hence, we have
$-\cos \left( B+C \right)=2\cos B\cos C$
We know that $\cos \left( x+y \right)=\cos x\cos y-\sin x\sin y$
Hence, we have
$\begin{aligned} & -\left( \cos B\cos C-\sin B\sin C \right)=2\cos B\cos C \\\ & \Rightarrow \sin B\sin C-\cos B\cos C=2\cos B\cos C \\\ \end{aligned}$
Dividing both sides by cosBcosC, we get
$\dfrac{\sin B\sin C}{\cos B\cos C}-1=2$
We know that $\dfrac{\sin x}{\cos x}=\tan x$
Hence, we have
$\tan B\tan C-1=2$
Adding 1 on both sides, we get
$\tan B\tan C=3$
Hence tanBtanC = 3
Hence option [a] is correct.

Note: Alternative Solution:
This solution is without using some already derived results. It is using basic geometry and trigonometry.
We know that the image of orthocentre lies on the circumcircle.

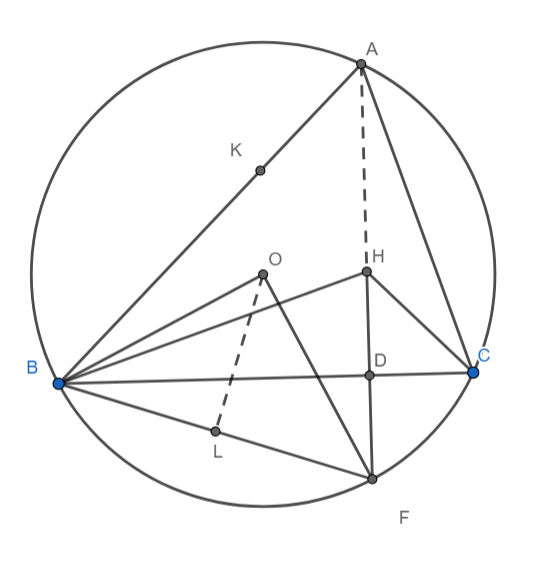
Hence produce HD and let it intersect circumcircle at F. Join OF and draw OL perpendicular to BF.
Now, we have
In right-angled triangle ADC,
$\begin{aligned} & C+\angle DAC=90{}^\circ \\\ & \Rightarrow \angle DAC=90{}^\circ -C \\\ \end{aligned}$
Now, we have
$\begin{aligned} & \angle BAF+\angle DAC=A \\\ & \Rightarrow \angle BAF=A-\left( 90{}^\circ -C \right)=A+C-90{}^\circ \\\ \end{aligned}$
We know that the angle subtended by the chord at the centre is twice the angle subtended in the alternate segment.
Hence, we have
$\angle BOF=2\angle BAF$
But, we know that $\angle BOF=2\angle BOL$
Hence, we have
$\begin{aligned} & 2\angle BOL=2\left( A+C-90{}^\circ \right) \\\ & \Rightarrow \angle BOL=A+C-90{}^\circ \\\ \end{aligned}$
Hence from right-angled triangle BOL, we have
$BL=R\sin \left( A+C-90{}^\circ \right)=R\sin \left( 180{}^\circ -B-90{}^\circ \right)=R\cos B$
Hence we have
$BF=2BL=2R\cos B$
Also, we have $\angle HBD=90{}^\circ -C$(Follow a similar procedure as shown for angle CAD) and HD = RcosA
Hence, we have
$BH=HD\csc \left( 90{}^\circ -C \right)=R\cos A\sec C$
But BF = BH, since F is the mirror image of H.
Hence, we have
$R\cos A\sec C=2R\cos B$
Multiplying both sides by cosC, we get
$R\cos A=2R\cos A\cos B$, which is the same as obtained above. Hence following a similar procedure as above, we get tanBtanC = 3.
Hence option [c] is correct.