Question

In a triangle ABC , sinA , sinB , sinC are in AP then
The altitudes are in AP
The altitudes are in HP
The angles are in AP
The angles are in HP

Answer 1

Hint - In such questions representing all the three sides a , b , c in terms of a constant like area of the triangle would be used to find the relation between all the sides . Using what is given in the question with the sine formula would give you the desired result .

Complete step-by-step answer:

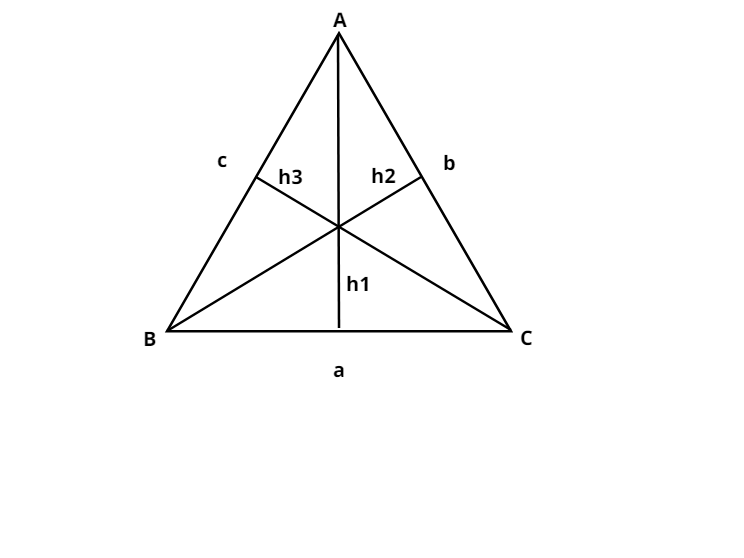
Let us consider the triangle ABC with sides a, b, c and altitude ${h_1},{h_2},{h_3}$ upon the base BC , AC , AB respectively .
Let the area of the triangle ABC be R
R = $\dfrac{1}{2}$ $\left( {{h_1} \times a} \right)$ = $\dfrac{1}{2}$ $\left( {{h_2} \times b} \right)$ = $\dfrac{1}{2}$ $\left( {{h_3} \times c} \right)$
( area of the triangle = $\dfrac{1}{2}$ base $\times$ height )
$\Rightarrow$ $a = \dfrac{{2R}}{{{h_1}}};b = \dfrac{{2R}}{{{h_2}}};c = \dfrac{{2R}}{{{h_3}}}$

Now using the sine formula
$\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}}$ = k (constant)
$\Rightarrow$ sinA = $\dfrac{a}{k}$ ; sinB = $\dfrac{b}{k}$ ; sinC = $\dfrac{c}{k}$
$$$$
Now according to the question sinA , sinB , sinC are in AP
$\Rightarrow$ $\dfrac{a}{k},\dfrac{b}{k},\dfrac{c}{k}$ are in AP

Now , putting values of a , b , c from above ,
$\dfrac{1}{{{h_1}}}\dfrac{{2R}}{k};\dfrac{1}{{{h_2}}}\dfrac{{2R}}{k};\dfrac{1}{{{h_3}}}\dfrac{{2R}}{k}$ are in AP
$\Rightarrow$ $\dfrac{1}{{{h_1}}};\dfrac{1}{{{h_2}}};\dfrac{1}{{{h_3}}}$ are in AP ( cancelling out the constants )
Therefore ,
${h_1},{h_2},{h_3}$ are in HP
Altitudes are in HP .

Note -
In these questions it is suitable to find an indirect method rather than to directly solve what's given . Remember that each fraction in the Sine Rule formula should contain a side and its opposite angle. Note that you should try and keep full accuracy until the end of your calculation to avoid errors .
$\Rightarrow$ $\dfrac{1}{{{h_1}}};\dfrac{1}{{{h_2}}};\dfrac{1}{{{h_3}}}$ are in AP ( cancelling out the constants )
Therefore ,
${h_1},{h_2},{h_3}$ are in HP
Altitudes are in HP .