Question

In a triangle ABC right angled at B, $\angle A=\angle C$, find the values of $\sin A\cos C+\cos A\sin C$.

Answer 1

Hint:We know that the sum of all the angles of a triangle is equal to $180{}^\circ$, so, $\angle A+\angle B+\angle C=180{}^\circ$. We will find the values of A and C and then we will put this value in the given relation, $\sin A\cos C+\cos A\sin C$ to get the value of the given trigonometric expression.

Complete step-by-step answer:
It is given in the question that ABC is a right angled triangle and $\angle B=90{}^\circ$. It is also given that angle A and angle C are equal and we have to find the value of the trigonometric expression, $\sin A\cos C+\cos A\sin C$. Now, we know that in a right angled triangle ABC, the sum of all the three angles of the triangle is equal to $180{}^\circ$. So, it means that,
$\angle A+\angle B+\angle C=180{}^\circ \ldots \ldots \ldots \left( i \right)$
It is also mentioned in the question that $\angle B=90{}^\circ$. So, we can draw the figure for the same as given below.

So, we can substitute the value of angle B, that is, $\angle B=90{}^\circ$ in equation (i). So, by doing the same, we get the equation as follows,
$\begin{aligned} & \angle A+\angle C+90{}^\circ =180{}^\circ \\\ & \Rightarrow \angle A+\angle C=180{}^\circ -90{}^\circ \\\ & \Rightarrow \angle A+\angle C=90{}^\circ \\\ \end{aligned}$
Now, we know that, $\angle A=\angle C$, as it is given in the question. So, we can write the same. So, we get,
$\begin{aligned} & \angle C+\angle C=90{}^\circ \\\ & \Rightarrow 2\angle C=90{}^\circ \\\ & \Rightarrow \angle C=\dfrac{90{}^\circ }{2} \\\ & \Rightarrow \angle C=45{}^\circ \\\ \end{aligned}$
So, since $\angle C=45{}^\circ$, $\angle A$ will also be equal to $45{}^\circ$. Now, we have the given relation as,
$\sin A\cos C+\cos A\sin C$
Let us write the standard trigonometric angles

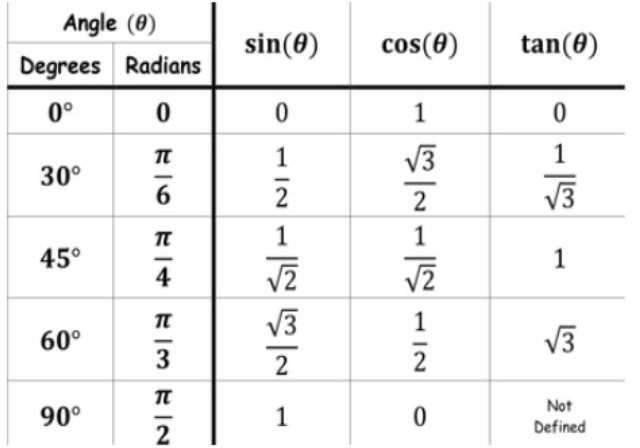
So, by substituting the values of $C=45{}^\circ$and $A=45{}^\circ$ in the above relation, we get,
$\sin 45{}^\circ \cos 45{}^\circ +\cos 45{}^\circ \sin 45{}^\circ$
We know that the value of $\sin 45{}^\circ =\dfrac{1}{\sqrt{2}}$ and the value of $\cos 45{}^\circ =\dfrac{1}{\sqrt{2}}$. So, by substituting these values in the above expression, we get,
$\begin{aligned} & \dfrac{1}{\sqrt{2}}\times \dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}\times \dfrac{1}{\sqrt{2}} \\\ & \Rightarrow \dfrac{1}{2}+\dfrac{1}{2}=1 \\\ \end{aligned}$
Hence, the value of the given expression, $\sin A\cos C+\cos A\sin C$ is 1.

Note: There is a possibility of committing a calculation mistake in the last step. In a hurry, the students may write, $\dfrac{1}{\sqrt{2}}\times \dfrac{1}{\sqrt{2}}\times \dfrac{1}{\sqrt{2}}\times \dfrac{1}{\sqrt{2}}$, which would change the answer completely. So, the students should be careful while substituting the values of the angles and they should remember a few of the trigonometric values of the standard angles.