Question

In a triangle ABC, let H, I and O be the orthocentre, incentre and circumcentre, respectively. If the points B, H, I, C lie on a circle, what is the magnitude of $\angle BOC$ in degrees.

Answer 1

Hint: See it is not possible to draw a diagram with all the things mentioned in the above question. So, draw the triangles with one special point like orthocentre at a time and deduce the results from it. Do the same for all the situations. You need to use the property that the angle subtended by a side of the triangle at the orthocentre id supplementary with the opposite interior angle. Also, you need to use that the angle subtended by a side at the incentre is $90{}^\circ$ more than the half of the opposite interior angle. Also, the property that the angle subtended by an arc at the circumference of the circle is equal and half of the angle subtended at the centre.

Complete step by step solution:
As we can realise that drawing a diagram with all the features mentioned in the question manually is not feasible. So, we will draw the figures part by part and keep on deducing the required result from each. First let us go for the Orthocentre.

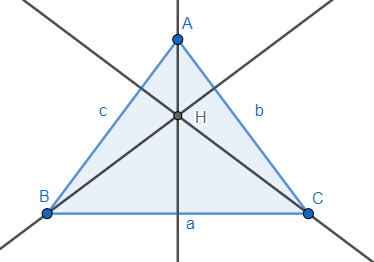
Now, we know that the angle subtended by a side of the triangle at the orthocentre is supplementary with the opposite interior angle.
$\angle BHC=180{}^\circ -\angle BAC............(i)$
Now let us move to the incentre.

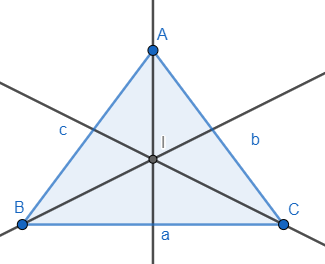
We also know that the angle subtended by a side at the incentre is $90{}^\circ$ more than the half of the opposite interior angle.
$\angle BIC=90{}^\circ -\dfrac{1}{2}\times \angle BAC.....(ii)$
Now let us move to the circumcentre of the triangle.

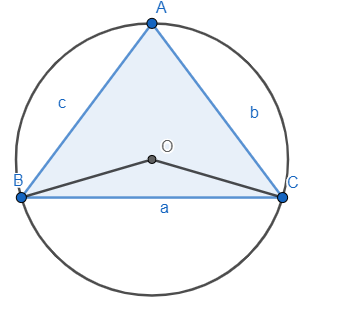
Also, we know that the angle subtended by an arc at the circumference of the circle is equal and half of the angle subtended at the centre.
$\angle BOC=2\times \angle BAC............(iii)$
Now let us move to the circle passing through the points B, H, I, C.

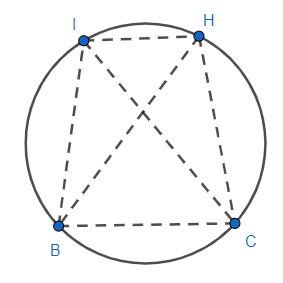
Again, using the property that the angle subtended by an arc at the circumference of the circle is equal and half of the angle subtended at the centre.
$\angle BHC=\angle BIC...........(iv)$
If we substitute angle BHC from equation (i) and angle BIC from equation (ii), we get
$180{}^\circ -\angle BAC=90{}^\circ +\dfrac{1}{2}\times \angle BAC$
$\Rightarrow 90{}^\circ =\dfrac{3}{2}\times \angle BAC$
Now we will use equation (iii) to substitute angle BAC. On doing so, we get
$90{}^\circ =\dfrac{3}{4}\times \angle BOC$
$\Rightarrow \angle BOC=120{}^\circ$
Hence, the answer to the above question is $\angle BOC=120{}^\circ$

Note: Remember, the centre of the largest circle that fits inside a triangle is called the incentre and is defined as the meeting point of all three angle bisectors of the triangle. Similarly, circumcentre is the meet point of the perpendicular bisectors of each side of the triangle, while orthocentre is the meet point of the altitudes of a triangle.