Question

In a triangle ABC, E is the midpoint of median AD. Show that $area({\text{BED) = }}\frac{1}{4}area({\text{ABC)}}{\text{.}}$

Answer 1

Hint: - Here we go through the properties of the median of the triangle to prove the question.As we know that the median of the triangle bisects the triangle into two equal parts.

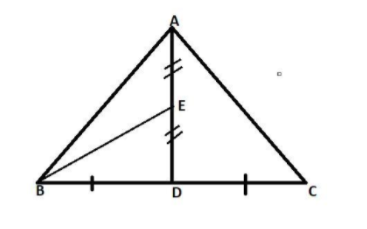
Here in the question it is given that,
AD is the median on BC of $\vartriangle {\text{ABC}}$ and we know that the median divides the triangle in two equal parts.
$\therefore area(\vartriangle {\text{ABD) = }}area(\vartriangle {\text{ACD)}}{\text{.}}$
It is also written as,
$\therefore area(\vartriangle {\text{ABD) = }}area(\vartriangle {\text{ACD) = }}\frac{1}{2}area(\vartriangle {\text{ABC)}}$……… (1)
Now in the question it is given that EB is the median on AD of$\vartriangle {\text{ABD}}$.
$\therefore area(\vartriangle {\text{BED) = }}area(\vartriangle {\text{BEA)}}$ As we know the property of the median above.
And it is also written as,
$\therefore area(\vartriangle {\text{BED) = }}area(\vartriangle {\text{BEA) = }}\frac{1}{2}area(\vartriangle {\text{ABD)}}$………… (2)
By the equation (1) and (2) we can write,

$\therefore area(\vartriangle {\text{BED) = }}\frac{1}{2} \times \frac{1}{2}area(\vartriangle {\text{ABC)}}$ $\because area(\vartriangle {\text{ABD) = }}\frac{1}{2}area(\vartriangle {\text{ABC)}}$
As we proved above.
$\therefore area(\vartriangle {\text{BED) = }}\frac{1}{4}area(\vartriangle {\text{ABC)}}$ Hence, proved.

Note: - Whenever we face such a type of question the key concept of solving the question is to first make the diagram and name it as given in the question. Then apply the property of that statement which is given in the question here in this question we apply the property of median.