Question

In a triangle ABC, D divides BC in the ratio of 3:2 and E divides CA in the ratio of 1:3. The lines AD and BE meet at H and CH meets AB in F. Find the ratio in which F divides AB.
A. $AF:FB = 2:1$
B. $AF:FB = 1:2$
C. $AF:FB = 2:3$
D. $AF:FB = 3:2$

Answer 1

In order to solve this problem we need to be familiar with few concepts in vector mathematics. Here one of the most important and crucial formulas is used from vector math which is the position vector formula. If a point divides a line PQ in the ratio of m:n, then the position vector of that particular point is given by the ratio of addition of product of m and Q plus product of n and P to the addition of m and n, given below:
$\Rightarrow \dfrac{{mQ + nP}}{{m + n}}$ is the position vector of the point which divides the line PQ internally.

Complete step-by-step solution:
Given that there is a triangle ABC, and we visualizing it as given below:

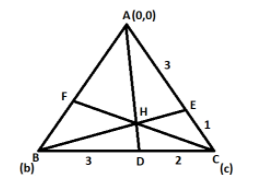
Given that the point D divides the side AC in the ratio of 3:2.
Also given that the point E divides the side AC in the ratio of 3:1.
H is the point of intersection of the lines AD and BE along with CF, where F divides the side AB and we have to find in what ratio F divides the line AB.
Consider that the vertex A is at the origin (0,0).
The points B and C have the position vectors as b and c respectively.
Now applying the position vector formula here at the point D which divides the side BC in the ratio of 3:2, as given below:
The position vector of point D is given by:
$\Rightarrow D = \dfrac{{3(c) + 2(b)}}{{3 + 2}}$
$\Rightarrow D = \dfrac{{3c + 2b}}{5}$
Now applying the position vector formula here at the point E, as it divides the side BC in the ratio of 3:2, as given below:
The position vector of point E is given by:
$\Rightarrow E = \dfrac{{3(c) + 1(0,0)}}{{3 + 1}}$
$\Rightarrow E = \dfrac{{3c}}{4}$
Now let us consider that the point H divides the line AD in the ratio of $t:1 - t$, applying the position vector formula at H on the line AD, as given below:
$\Rightarrow AD = \dfrac{{t(D) + 1 - t(0,0)}}{{t + 1 - t}}$
We know that the position of $D = \dfrac{{3c + 2b}}{5}$, substituting it in the AD equation, as given below:
$\Rightarrow AD = t\left( {\dfrac{{3c + 2b}}{5}} \right)$
$\Rightarrow AD = \dfrac{{3t}}{5}c + \dfrac{{2t}}{5}b$
Now let us consider that the point H divides the line BE in the ratio of $s:1 - s$, applying the position vector formula at H on the line BE, as given below:
$\Rightarrow BE = \dfrac{{s(E) + (1 - s)b}}{{s + 1 - s}}$
We know that the position of $E = \dfrac{{3c}}{4}$, substituting it in the BE equation, as given below:
$\Rightarrow BE = s\left( {\dfrac{{3c}}{4}} \right) + (1 - s)b$
$\Rightarrow BE = \dfrac{{3s}}{4}c + (1 - s)b$
Now the lines BE and AD intersect at H. Hence equating the position vectors of H on BE and AD, as given below:
$\Rightarrow \dfrac{{3t}}{5}c + \dfrac{{2t}}{5}b = \dfrac{{3s}}{4}c + (1 - s)b$
In the above expression comparing the coefficients of b and c, as given below:
Equating the coefficients of c, as given below:
$\Rightarrow \dfrac{{3t}}{5} = \dfrac{{3s}}{4}$
$\Rightarrow t = \dfrac{{5s}}{4}$
Now equating the coefficients of b, as given below:
$\Rightarrow \dfrac{{2t}}{5} = 1 - s$
So now we have two equations and two variables s and t, solving the two equations to get the values of t and s, as given below:
Substituting the value of t, $t = \dfrac{{5s}}{4}$ in the expression $\dfrac{{2t}}{5} = 1 - s$, gives:
$\Rightarrow \dfrac{2}{5}\left( {\dfrac{{5s}}{4}} \right) = 1 - s$
$\Rightarrow \dfrac{s}{2} = 1 - s$
$\Rightarrow s = \dfrac{2}{3}$
Substituting this obtained expression in the t expression in order to get the value of t, as given:
$\Rightarrow \;t = \dfrac{5}{6}$
$\therefore s = \dfrac{2}{3}$ and hence, $(1 - s) = \dfrac{1}{3}$
$\therefore t = \dfrac{5}{6}$ and hence, $(1 - t) = \dfrac{1}{6}$
Now substitute these values in the position vector of on AD, as given below:
$\Rightarrow H = t\left( {\dfrac{{3c + 2b}}{5}} \right)$
$\Rightarrow H = \dfrac{5}{6}\left( {\dfrac{{3c + 2b}}{5}} \right)$
$\Rightarrow H = \dfrac{{3c + 2b}}{6}$
Now consider the point F on AB as it is given that it is a point of intersection of AB and CH.
Consider that F divides the line AB in the ratio of $p:1 - p$, applying the position vector formula at F on the line AB, as given below:
$\Rightarrow AB = \dfrac{{p(B) + (1 - p)(0,0)}}{{p + 1 - p}}$
$\Rightarrow AB = pb$
Now let us consider that the point F divides the line CH in the ratio of $r:1 - r$, applying the position vector formula at F on the line CH, as given below:
$\Rightarrow CH = \dfrac{{r(H) + (1 - r)C}}{{r + 1 - r}}$
We know that the position vector of H is $H = \dfrac{{3c + 2b}}{6}$, substituting it, as given below:
$\Rightarrow CH = r\left( {\dfrac{{3c + 2b}}{6}} \right) + (1 - r)c$
$\Rightarrow CH = \left( {\dfrac{{3r}}{6} + (1 - r)} \right)c + \dfrac{{2r}}{6}b$
Now their point of intersection is F, equating them in order to find the values of s and r, as given:
$\Rightarrow pb = \left( {\dfrac{{3r}}{6} + (1 - r)} \right)c + \dfrac{{2r}}{6}b$
In the above expression comparing the coefficients of b and c, as given below:
Equating the coefficients of c, as given below:
$\Rightarrow \dfrac{{3r}}{6} + (1 - r) = 0$
$\Rightarrow \dfrac{r}{2} = 1$
$\Rightarrow r = 2$
Now equating the coefficients of b, as given below:
$\Rightarrow p = \dfrac{{2r}}{6}$
$\Rightarrow p = \dfrac{r}{3}$
Substituting the value of r in the above expression to get the value of p, as given below:
$\Rightarrow p = \dfrac{2}{3}$
$\therefore p = \dfrac{2}{3}$ and hence, $1 - p = \dfrac{1}{3}$
As we already discussed F divides the side AB in the ratio of $p:1 - p$, which is now given by:
The point F divides AB in the ratio of $\dfrac{2}{3}:\dfrac{1}{3}$, which is equal to $2:1$.
$\therefore$F divides AB in the ratio of $2:1$.

Option A is the correct answer.

Note: It is important to remember when and how to apply the position vector, here when a line is internally divided then the position vector formula of $\overline r = \dfrac{{m\overline b + n\overline a }}{{m + n}}$ is applied, whereas if the line is divided externally then the position vector formula to be applied would be $\overline r = \dfrac{{m\overline b - n\overline a }}{{m - n}}$.