Question

In a triangle ABC, $\angle C = {90^ \circ }$, a = 3, b = 4 and D is a point on AB, so that $\angle BCD = {30^ \circ }$, Then the length of CD is,
$\left( a \right)\dfrac{{18 - 24\sqrt 3 }}{{25}}$
$\left( b \right)\dfrac{{18 + 24\sqrt 3 }}{{25}}$
$\left( c \right)\dfrac{{8 - 24\sqrt 3 }}{{25}}$
$\left( d \right)$ None of these

Answer 1

Hint: In this particular type of question draw the perpendicular from point D on line BC and AC which intersect the line at point E and F as shown in the below figure and use the concept that in a right angle triangle sine of angle is the ratio of perpendicular to hypotenuse so using this calculate the length of the perpendicular drawn so use these concepts to reach the solution of the question.

Complete step-by-step answer:

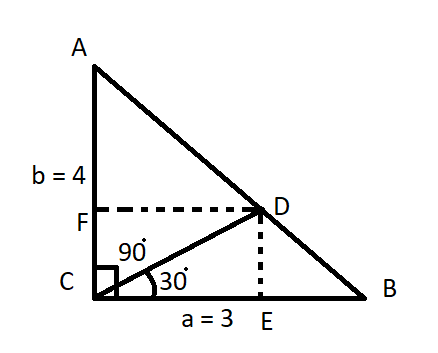
The pictorial representation of the given problem is shown above.
It is given that $\angle C = {90^ \circ }$ and a = 3, b = 4 as shown in the figure.
D is a point on line AB such that $\angle BCD = {30^ \circ }$ as shown in the figure.
So, $\angle DCA = \angle ACB - \angle BCD = {90^ \circ } - {30^ \circ } = {60^ \circ }$
Now draw the perpendicular from point D on line BC and AC which intersect the line at point E and F as shown in the figure.
So in triangle CDE we know that sine is the ratio of perpendicular to hypotenuse so we have,
$\Rightarrow \sin {30^ \circ } = \dfrac{{DE}}{{CD}}$
$\Rightarrow DE = CD\sin {30^ \circ }$.............. (1)
Similarly in triangle CDF we have,
$\Rightarrow \sin {60^ \circ } = \dfrac{{DF}}{{CD}}$
$\Rightarrow DF = CD\sin {60^ \circ }$.............. (2)
Now as we know that the area of the triangle is given as,
$\Rightarrow {\text{Area = }}\dfrac{1}{2}\left( {{\text{base}}} \right)\left( {{\text{height}}} \right)$
So from figure, the area of the triangle ABC = area of triangle BCD + area of triangle ACD.
Therefore,
$\Rightarrow \dfrac{1}{2}\left( {{\text{BC}}} \right)\left( {{\text{AC}}} \right) = \dfrac{1}{2}\left( {{\text{BC}}} \right)\left( {{\text{DE}}} \right) + \dfrac{1}{2}\left( {{\text{AC}}} \right)\left( {{\text{DF}}} \right)$
Now substitute the values we have,
$\Rightarrow \dfrac{1}{2}\left( {\text{3}} \right)\left( {\text{4}} \right) = \dfrac{1}{2}\left( {\text{3}} \right)\left( {{\text{CDsin3}}{{\text{0}}^ \circ }} \right) + \dfrac{1}{2}\left( {\text{4}} \right)\left( {{\text{CDsin6}}{{\text{0}}^ \circ }} \right)$
Now as we know that the value of ${\text{sin3}}{{\text{0}}^ \circ } = \dfrac{1}{2}{\text{ and sin6}}{{\text{0}}^ \circ } = \dfrac{{\sqrt 3 }}{2}$ so we have,
$\Rightarrow \dfrac{1}{2}\left( {\text{3}} \right)\left( {\text{4}} \right) = \dfrac{1}{2}\left( {\text{3}} \right)\left( {\dfrac{{{\text{CD}}}}{2}} \right) + \dfrac{1}{2}\left( {\text{4}} \right)\left( {\dfrac{{{\text{CD}}\sqrt 3 }}{2}} \right)$
Now simplify we have,
$\Rightarrow 12 = \dfrac{{3CD}}{2} + 2\sqrt 3 CD$
$\Rightarrow 12 = \left( {\dfrac{{3 + 4\sqrt 3 }}{2}} \right)CD$
$\Rightarrow CD = \dfrac{{24}}{{3 + 4\sqrt 3 }}$
So this is the required length of CD.
Hence option (D) none of these is the required answer.

Note – Whenever we face such types of questions the key concept we have to remember is that always recall that the area of triangle is half multiplied by the base times the height, so the area of the triangle ABC = area of triangle BCD + area of triangle ACD so substitute all the values in this as above and simplify we will get the required answer.