Question

In a triangle ABC, AD is the bisector of angle A meeting BC at D. If I is the in-centre of the triangle, then $AI:DI$ is, $$$$
A. \left( \sin B+ \sin C \right):\sin A$$$$$ B. \left( \cos B+ \cos C \right):\sin A C. $\cos \left( \dfrac{B-C}{2} \right):\cos \left( \dfrac{B+C}{2} \right)
D. $\sin \left( \dfrac{B-C}{2} \right):\sin \left( \dfrac{B+C}{2} \right)$$$$$

Answer 1

We join BI and CI. We use angle bisector theorem for the angles $\angle ABD,\angle ACD$ in triangle ABD and ACD to get $\dfrac{AI}{DI}=\dfrac{b+c}{a}$ where $a=BC,b=AC,c=AB$. We use sine law of triangle $\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$ and the identities $\sin C+\sin D=2\sin \left( \dfrac{C+D}{2} \right)\cos \left( \dfrac{C-D}{2} \right)$,$\sin 2\theta =2\sin \theta \cos \theta$ to choose the correct options. $$$$

Complete step-by-step solution:

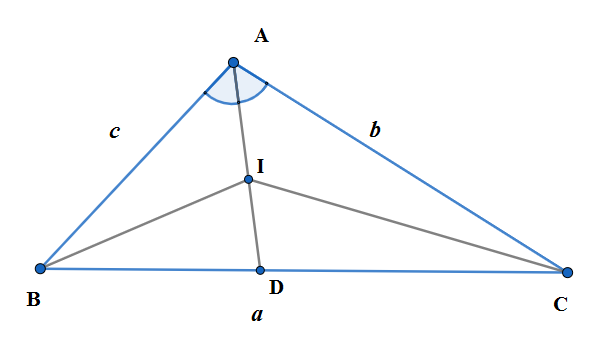
Let us denote the lengths of the sides as $AB=c,BC=a,AC=b$. Let us join BI and CI. We know from the angle bisector theorem, which states that the angle bisector divides the opposite side in a ratio equal to the ratio of lengths of corresponding adjacent sides of the angle. We use the angle bisector theorem in triangle ABD for the bisector BI of the $\angle ABD$ which divides the opposite side AD into AI and DI and has adjacent sides AB and BD respectively . We have

& \dfrac{AI}{DI}=\dfrac{AB}{BD} \\\ & \Rightarrow \dfrac{AI}{DI}=\dfrac{c}{BD}.....\left( 1 \right) \\\ \end{aligned}$$ We again use the angle bisector theorem in triangle ABD for the bisector BI of the $\angle ACD$ which divides the opposite side AD into AI and DI and has adjacent sides are AC and CD respectively. We have $$\begin{aligned} & \dfrac{AI}{DI}=\dfrac{AC}{CD} \\\ & \Rightarrow \dfrac{AI}{DI}=\dfrac{b}{CD}.......\left( 2 \right) \\\ \end{aligned}$$ We equate right hand sides of (1) and (2) to have; $$\begin{aligned} & \dfrac{b}{CD}=\dfrac{c}{BD} \\\ & \Rightarrow \dfrac{b}{c}=\dfrac{CD}{BD}\left( \text{By alternendo} \right) \\\ \end{aligned}$$ We add both sides by 1 to have; $$\begin{aligned} & \Rightarrow \dfrac{b+c}{c}=\dfrac{CD+BD}{BD} \\\ & \Rightarrow \dfrac{b+c}{c}=\dfrac{BC}{BD} \\\ & \Rightarrow \dfrac{b+c}{c}=\dfrac{a}{BD} \\\ & \Rightarrow \dfrac{b+c}{a}=\dfrac{c}{BD}......\left( 3 \right) \\\ \end{aligned}$$ We have from (1) and (3) $$\dfrac{AI}{DI}=\dfrac{b+c}{a}.......\left( 4 \right)$$ We know from sine law that the lengths of triangle and sine of the angle of the opposite sides are always in proportion. It means; $$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R$$ Here $R$ is the circum-radius of the triangle. So we have; $$a=2R\sin A,b=2R \sin B,c=2R \sin C$$ We put the above values in (4) to have; $$\begin{aligned} & \dfrac{AI}{DI}=\dfrac{2R\sin B+2R\sin C}{2R\sin A} \\\ & \Rightarrow \dfrac{AI}{DI}=\dfrac{\sin B+\sin C}{\sin A}......\left( 5 \right) \\\ \end{aligned}$$ We use the identity $\sin C+\sin D=2\sin \left( \dfrac{C+D}{2} \right)\cos \left( \dfrac{C-D}{2} \right)$ for $C=A,D=C$ and teh sine double angle formula $\sin 2\theta =2\sin \theta \cos \theta $ for $\theta =\dfrac{A}{2}$ in the above step to have $$\dfrac{AI}{DI}=\dfrac{2\sin \left( \dfrac{B+C}{2} \right)\cos \left( \dfrac{B-C}{2} \right)}{2\sin \dfrac{A}{2}\cos \dfrac{A}{2}}$$ We know in a triangle $A+B+C=\pi $then we have $\dfrac{\pi }{2}-\dfrac{B+C}{2}=\dfrac{A}{2}$. We have $$\begin{aligned} & \Rightarrow \dfrac{AI}{DI}=\dfrac{\sin \left( \dfrac{B+C}{2} \right)\cos \left( \dfrac{B-C}{2} \right)}{\sin \left( \dfrac{\pi }{2}-\dfrac{B+C}{2} \right)\cos \left( \dfrac{\pi }{2}-\dfrac{B+C}{2} \right)} \\\ & \Rightarrow \dfrac{AI}{DI}=\dfrac{\sin \left( \dfrac{B+C}{2} \right)\cos \left( \dfrac{B-C}{2} \right)}{\cos \left( \dfrac{B+C}{2} \right)\sin \left( \dfrac{B+C}{2} \right)} \\\ & \Rightarrow \dfrac{AI}{DI}=\dfrac{\cos \left( \dfrac{B-C}{2} \right)}{\cos \left( \dfrac{B+C}{2} \right)}....\left( 6 \right) \\\ \end{aligned}$$ We have from (5) and (6) $$AI:DI=\left( \sin B+\sin C \right):\sin A=\cos \left( \dfrac{B-C}{2} \right):\cos \left( \dfrac{B+C}{2} \right)$$ **So the correct options are A and C.** **Note:** We can alternatively use the theorem that the in-centre divides the angle bisector in ratio that is equal to the ratio of sum of the lengths of adjacent sides to the opposite sides to directly get $\dfrac{AI}{DI}=\dfrac{b+c}{a}$. We note that in-centre is the point of intersection of angle bisectors and circum-centre is the point of intersection of perpendicular bisectors of sides