Question
Question: In a triangle ABC, AD is altitude from A. Given b\>c, \(\angle C = 23 ^ { \circ }\) and \(A D = \fr...
In a triangle ABC, AD is altitude from A. Given b>c,
∠C=23∘ and AD=b2−c2abc then ∠B equal to
A
67∘
B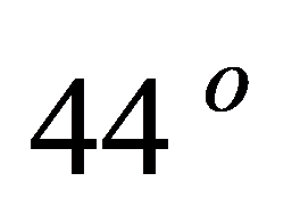
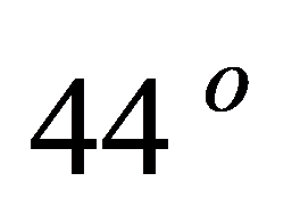
C
113∘
D
None of these
Answer
113∘
Explanation
Solution
cosB=2aca2+c2−b2=2aca2−(b2−c2)
Now, AD=b2−c2abc ; ∴ cosB=2aca2−ADabc
Also AD=bsin23∘ ; ∴cosB=2ca−sin23∘c
By sine formulae ⇒ ca=sin23∘sin(B+23∘) ;
∴ cosB=2[sin23∘sin(B+23∘)−sin23∘1]
⇒ sin(23∘−B)=−1=sin(−90∘) ; therefore 23∘−B=−90∘ or
B=113∘.
