Question

In a thin spherical fish bowl of radius $10cm$ filled with water of refractive index $\dfrac{4}{3}$ there is a small fish at a distance of $4cm$ from the center $C$ as shown in figure. Where will the image of the fish appears, if seen from E
A. $5.2cm$
B. $7.2cm$
C. $4.2cm$
D. $3.2cm$

Answer 1

here, we will consider the spherical fish bowl as a spherical surface in which the object is taken as fish. Here, there will be two mediums, one from which the image will be seen and the other in which the image will be made. Here, we will use the refraction formula of the spherical surface to calculate the distance of the image.

Formula used:
The formula of refraction of spherical surface is given by
$\dfrac{{{n_2}}}{v} - \dfrac{{{n_1}}}{u} = \dfrac{{{n_2} - {n_1}}}{R}$
Here, ${n_2}$ is the refractive index of the second medium, ${n_1}$ is the refractive index of the first medium, $v$ is the distance of the image from the mirror, $u$ is the distance of the object from the mirror and $R$ is the radius of the surface.

Complete step by step answer:
Consider a spherical fish bowl of radius $10cm$ filled with water as shown below

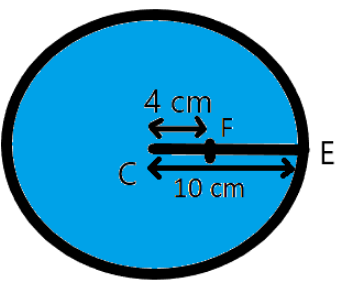
Here, $C$ is the center of the spherical bowl, $F$ is the position of fish which is $4cm$ away from the center and $E$ is the point from which we will see the image of the fish.
Here, the refractive index of water is $\dfrac{4}{3}$ . also let refractive index of air is $1$ .
Here, the distance of the fish from the center is, $= 4cm$
Therefore, the distance of the fish from the surface, $u = 6cm$
Also, the radius of the bowl is, $R = 10cm$
Now, using the refraction formula at spherical surface which is given below
$\dfrac{{{n_2}}}{v} - \dfrac{{{n_1}}}{u} = \dfrac{{{n_2} - {n_1}}}{R}$
Here, ${n_2}$ is the refractive index of the air and ${n_1}$ is the refractive index of the water.
Putting the values in the above equation, we get
$\dfrac{1}{v} - \dfrac{{\dfrac{4}{3}}}{{ - 6}} = \dfrac{{1 - \dfrac{4}{3}}}{{ - 10}}$
$\Rightarrow \,\dfrac{1}{v} + \dfrac{4}{{18}} = \dfrac{{\dfrac{{ - 1}}{3}}}{{10}}$
$\Rightarrow \,\dfrac{1}{v} = \dfrac{1}{{30}} - \dfrac{4}{{18}}$
$\Rightarrow \,\dfrac{1}{v} = \dfrac{{3 - 20}}{{90}}$
$\Rightarrow \,\dfrac{1}{v} = \dfrac{{ - 17}}{{90}}$
$\Rightarrow \,v = \dfrac{{ - 90}}{{17}} = - 5.2$
Taking magnitude, we get
$\therefore v = 5.2cm$
Therefore, the image will be at a distance of $5.2cm$ from the point $E$ .

Hence, option A is the correct option.

Note: Here we have taken two surfaces, because the image will be formed in the water and it will be seen in the air. Also, we have taken the distance of image and the radius as negative, because we have taken these values in the negative X-direction (if we take the point $E$ as origin). Also, we got the answer in the negative, which means that we will get an image somewhere in the negative X-direction.