Question
Question: In a thick glass slab of thickness \(I\), and refractive index \({n_1}\), a cuboidal cavity of thick...
In a thick glass slab of thickness I, and refractive index n1, a cuboidal cavity of thickness m as curved as shown in Fig and is filled with a liquid of refractive index n2(n1>n2). The ratio ml, so that shift produced by this slab is zero when an observer A observes B with paraxial rays is:
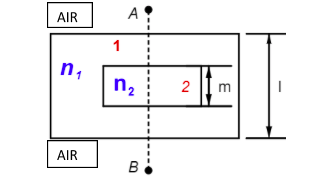
A) n2−n1n1−n2
B) n2(n1−1)n1−n2
C) (n1−1)n1−n2
D) n1(n2−1)n1−n2
Solution
For this problem, we have to calculate shifts differently for the liquid in the cavity and the glass slab the refractive index(R.I) and the thickness are different.The total shift is given zero.
Formula used:
Shift due to cavity, x1=m(1−n21)where m= depth of cavity and n2= R.I of the liquid inside the cavity.
Shift due to the glass slab, x2=(l−m)(1−n11)where = the thickness of the glass slab and n1= R.I of the liquid inside the glass slab.
Total shift, x1+x2=0
Complete step by step answer:
The refractive index of an object =relative depth of the objectoriginal depth of the object from the separation plane
Therefore refractive index, n=d′d
Where d= original depth of the object from separation plane
d′= relative depth of the object from the separation plane
Now, as there is a concept of original depth and relative depth then there must be a virtual shift happening according to the observer.
This shift is defined by, shift=depth(1−R.I1).
Therefore, Shift due to cavity, x1=m(1−n21)
where m= thickness of cavity and n2= R.I of the liquid inside the cavity.
Shift due to the glass slab, x2=(l−m)(1−n11)
where I = the thickness of the glass slab and n1= R.I of the liquid inside the glass slab.
Given that total shift is zero i.e. x1+x2=0
So,
m(1−n21)+(l−m)(1−n11)=0
⇒m−n2m+(l−m)−n1(l−m)=0
⇒m−n2m+l−m−n1l+n1m=0
⇒l(1−n11)−m(n21−n11)=0
⇒l(1−n11)=m(n21−n11)
⇒l(n1n1−1)=m(n1n2n1−n2)
⇒l(n1−1)=m(n2n1−n2)
The ratio, ml=[n2(n1−1)n1−n2].
⇒ml=[n2(n1−1)n1−n2]
Hence, option (B) is the correct one.
Notes: When the object is in a denser medium and the observer is in a rarer medium, the refracted ray diverges from the normal of the plane. In this condition, the object seems raised from the separation plane.
When the object is in a rarer medium and the observer is in a denser medium, the refracted ray comes close to the normal of the plane. In this condition, the object seems to have gone far from the separation plane.
