Question

In a thermodynamic process on an ideal monatomic gas, the infinitesimal heat absorbed by the gas is given by $T\Delta X$, where T is temperature of the system and $\Delta X$ is the infinitesimal change in a thermodynamic quantity X of the system. For a mole of monatomic ideal gas $X=\dfrac{3}{2}R\ln \left( \dfrac{T}{{{T}_{A}}} \right)+R\ln \left( \dfrac{V}{{{V}_{A}}} \right)$. Here, R is gas constant, V is volume of gas, ${{T}_{A}}$and ${{V}_{A}}$are constants.
The List-I below gives some quantities involved in a process and List-II gives some possible values of these quantities.

List I	List II
I. Work done by the system in process $1\to 2\to 3$	P. $\dfrac{1}{3}R{{T}_{0}}\ln 2$
II. Change in internal energy in process $1\to 2\to 3$	Q. $\dfrac{1}{3}R{{T}_{0}}$
III. Heat absorbed by the system in process $1\to 2\to 3$	R. $R{{T}_{0}}$
IV. Heat absorbed by the system in process $1\to 2$	S. $\dfrac{4}{3}R{{T}_{0}}$
T. $\dfrac{1}{3}R{{T}_{0}}\left( 3+\ln 2 \right)$
U. $\dfrac{5}{6}R{{T}_{0}}$

If this process on one mole of monatomic ideal gas is as shown in the TV-diagram with ${{P}_{0}}{{V}_{0}}=\dfrac{1}{3}R{{T}_{0}}$.

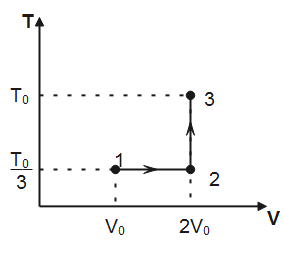
Which of the following is the correct match?
A. $I\to P,\,II\to R,\,III\to T,\,IV\to S$
B. $I\to P,\,II\to T,\,III\to Q,\,IV\to T$
C. $I\to P,\,II\to R,\,III\to T,\,IV\to P$
D. $I\to S,\,II\to T,\,III\to Q,\,IV\to U$

Answer 1

First analyze the type of process from the TV-diagram given. Then, calculate the work done, change in internal energy during each process and for the process $1\to 2\to 3$ as well. First law of thermodynamics can be used to determine the heat transferred during any process.
Formula used: In an isothermal process, $W=nRT\ln \dfrac{{{V}_{f}}}{{{V}_{i}}}$
In an isochoric process, $\Delta U=\dfrac{f}{2}nR\Delta T$
First law of thermodynamics, $Q=\Delta U+W$

Complete step by step answer:
Note that, in process $1\to 2$ temperature is constant hence, the process is isothermal. In process $2\to 3$, volume of the gas remains conserved, therefore, the process $2\to 3$ is isochoric. Degree of freedom for a monatomic gas, $f=3$

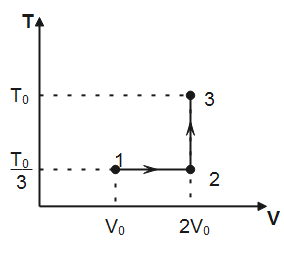
(I) Work done for isothermal process $1\to 2$ is given by
${{W}_{1\to 2}}=nRT\ln \dfrac{{{V}_{f}}}{{{V}_{i}}}$
Where $n$ is the number of moles of the gas, $T$ is the absolute temperature and ${{V}_{f}}\And \,\,{{V}_{i}}$ denotes final and initial volume of the gas respectively. Substituting the values observed from plot, we have
${{W}_{1\to 2}}=1\times R\times \dfrac{{{T}_{0}}}{3}\ln \dfrac{2{{V}_{0}}}{{{V}_{0}}}=\dfrac{R{{T}_{0}}}{3}\ln 2$
Work done for the isochoric process $2\to 3$ is zero. Since, no volume is changed during an isochoric process, the work done (which is linearly proportional to change in volume) is zero.
${{W}_{2\to 3}}=0$
Therefore, work done by the system in process $1\to 2\to 3$ is
${{W}_{1\to 2\to 3}}={{W}_{1\to 2}}+{{W}_{2\to 3}}=\dfrac{R{{T}_{0}}}{3}\ln 2+0=\dfrac{R{{T}_{0}}}{3}\ln 2$
This implies that $I\to P$
(II) Internal energy changed in process $1\to 2\to 3$ is given by
$\Delta {{U}_{1\to 2\to 3}}=\Delta {{U}_{1\to 2}}+\Delta {{U}_{2\to 3}}$
This implies that,
$\Delta {{U}_{1\to 2\to 3}}=\dfrac{f}{2}nR\Delta {{T}_{1\to 2}}+\dfrac{f}{2}nR\Delta {{T}_{2\to 3}}$
Substituting the values observed from the plot, we have
$\Delta {{U}_{1\to 2\to 3}}=\dfrac{f}{2}\times 1\times R\left( \dfrac{{{T}_{0}}}{3}-\dfrac{{{T}_{0}}}{3} \right)+\dfrac{f}{2}\times 1\times R\left( {{T}_{0}}-\dfrac{{{T}_{0}}}{3} \right)=\dfrac{3}{2}R\times \dfrac{2{{T}_{0}}}{3}$
Solving the above equation, we obtain
$\Delta {{U}_{1\to 2\to 3}}=R{{T}_{0}}$
This implies that $II\to R$
(III) According to the first law of thermodynamics, heat transferred in a thermodynamic process is the sum of change in internal energy of the system and work done by the system. That is,
${{Q}_{1\to 2\to 3}}=\Delta {{U}_{1\to 2\to 3}}+{{W}_{1\to 2\to 3}}$
Substituting the values, we obtained above, we have
${{Q}_{1\to 2\to 3}}=R{{T}_{0}}+\dfrac{R{{T}_{0}}}{3}\ln 2$
${{Q}_{1\to 2\to 3}}=\dfrac{R{{T}_{0}}}{3}\left( 3+\ln 2 \right)$
This implies that $III\to T$
(IV) Similarly, for process $1\to 2$
${{Q}_{1\to 2}}=\Delta {{U}_{1\to 2}}+{{W}_{1\to 2}}$
Substituting the values, we get
${{Q}_{1\to 2}}=0+\dfrac{R{{T}_{0}}}{3}\ln 2=\dfrac{R{{T}_{0}}}{3}\ln 2$
This implies that $IV\to P$

Hence, option D is correct.

Note: In TV-diagram, line parallel to horizontal axis shows an isothermal process and line parallel to vertical axis shows an isochoric process. The work done in an isochoric process is zero.
According to the first law of thermodynamics, heat transferred in a thermodynamic process is the sum of change in internal energy of the system and work done by the system. This law is based on conservation of energy.