Question

In a survey of${\text{600}}$ students in a school, ${\text{150}}$ students were found to be taking tea and ${\text{225}}$ taking coffee, ${\text{100}}$ were taking both tea and coffee. Find how many students were taking neither tea nor coffee?

Answer 1

Hint: - Divide the given numbers into separate categories using a venn diagram and try to get the total number of students who are actually taking tea and coffee so that we can subtract them from total.

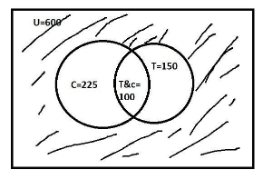
Let ${\text{U}}$ be the set of all students who took part in the survey.
Let ${\text{T}}$ be the set of students taking tea.
Let ${\text{C}}$ be the set of students taking coffee.
Now write these in the form of set,
$n(U) = 600,n(T) = 150,n(C) = 225,$
${\text{100}}$ Were taking both tea and coffee means $n(T \cap C) = 100$
To find Number of student taking neither tea nor coffee
I.e. we have to find$n(T' \cap C')$.
Here ${\text{T'}}$and ${\text{C'}}$ means not taking tea and coffee.
It means a total number of students$-$either taking tea or coffee.

$\Rightarrow n(T' \cap C'{\text{) = }}n(T \cup C)'$

And by set formula we know that $n(T \cup C) = [n(T) + n(C) - n(T \cap C)]$
$= n(U) - n(T \cup C) \\\ = n(U) - [n(T) + n(C) - n(T \cap C)] \\\ = 600 - [150 + 225 - 100] \\\ = 600 - 275 \\\ = 325 \\\$
Hence, ${\text{325}}$ students were taking neither tea nor coffee.

Note: - whenever we face such a type of question, we have to apply the property set for solving the question and we also make a venn diagram for easy solving. Here in this venn diagram you have to find the shaded region.